题目内容
已知a，b，c∈R，且三次方程f(x)=x3-ax2+bx-c=0有三个实根x1，x2，x3，
(Ⅰ)类比一元二次方程根与系数的关系，写出此方程根与系数的关系；
(Ⅱ)若a，b，c均大于零，试证明：x1，x2，x3都大于零；
(Ⅲ)若a∈Z，b∈Z且|b|＜2，f(x)在x=α，x=β处取得极值，且-1＜α＜0＜β＜1，试求此方程三个根两两不等时c的取值范围。
(Ⅰ)类比一元二次方程根与系数的关系，写出此方程根与系数的关系；
(Ⅱ)若a，b，c均大于零，试证明：x1，x2，x3都大于零；
(Ⅲ)若a∈Z，b∈Z且|b|＜2，f(x)在x=α，x=β处取得极值，且-1＜α＜0＜β＜1，试求此方程三个根两两不等时c的取值范围。
解：(Ⅰ)由已知，得x3-ax2+bx-c=(x-x1)(x-x2)(x-x3)，
比较两边系数，得a=x1+x2+x3，b=x1x2+x2x3+x3x1，c=x1x2x3；
(Ⅱ)证明：由c＞0，得x1，x2，x3三数中或全为正数或一正二负，
若为一正二负，不妨设x1＞0，x2＜0，x3＜0，
由x1+x2+x3=a＞0，得x1＞-(x2+x3)，
则x1(x2+x3)＜-(x2+x3)2，
又b=x1x2+x2x3+x3x1=x1(x2+x3)+x2x3＜-(x2+x3)2+x2x3
，
这与b＞0矛盾，所以x1，x2，x3全为正数．
(Ⅲ)令f(x)=x3-ax2+bx-c，要f(x)=0有三个不等的实数根，则函数f(x)有一个极大值和一个极小值，且极大值大于0，极小值小于0，
由已知，得f′(x)=3x2-2ax+b=0有两个不等的实根α，β，
∵-1＜α＜0＜β＜1，
∴
，
由①③，得b＞-3，
又|b|＜2，b＜0，
∴b=-1，将b=-1代入①③，得a=0，
∴f ′(x)=3x2-1，则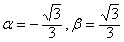
，
且f(x)在
处取得极大值，在
处取得极小值，
故f(x)=0要有三个不等的实数根，则必须
，得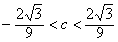
。
比较两边系数，得a=x1+x2+x3，b=x1x2+x2x3+x3x1，c=x1x2x3；
(Ⅱ)证明：由c＞0，得x1，x2，x3三数中或全为正数或一正二负，
若为一正二负，不妨设x1＞0，x2＜0，x3＜0，
由x1+x2+x3=a＞0，得x1＞-(x2+x3)，
则x1(x2+x3)＜-(x2+x3)2，
又b=x1x2+x2x3+x3x1=x1(x2+x3)+x2x3＜-(x2+x3)2+x2x3
，这与b＞0矛盾，所以x1，x2，x3全为正数．
(Ⅲ)令f(x)=x3-ax2+bx-c，要f(x)=0有三个不等的实数根，则函数f(x)有一个极大值和一个极小值，且极大值大于0，极小值小于0，
由已知，得f′(x)=3x2-2ax+b=0有两个不等的实根α，β，
∵-1＜α＜0＜β＜1，
∴
，由①③，得b＞-3，
又|b|＜2，b＜0，
∴b=-1，将b=-1代入①③，得a=0，
∴f ′(x)=3x2-1，则
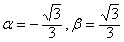，且f(x)在
处取得极大值，在处取得极小值，故f(x)=0要有三个不等的实数根，则必须
，得。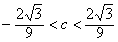
练习册系列答案
相关题目