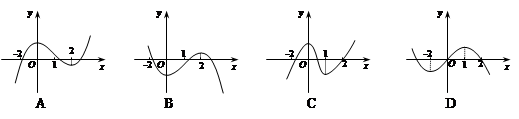题目内容
若函数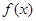 为奇函数,且当
为奇函数,且当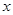 >0时
>0时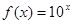 ,则
,则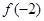 的值是( )
的值是( )
A.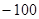 | B.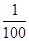  | C.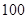 | D.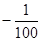 |
A
解析试题分析:先根据函数f(x)是R上的奇函数将f(-2)转化成求f(2)的值,代入当x>0时f(x)的解析式中即可求出所求.解:函数f(x)是R上的奇函数则f(-x)=-f(x),∴f(-2)=-f(2)∵当x>0时,f(x)=10x,∴f(2)=100则f(-2)=-f(2)=-100故选:A
考点:函数奇偶性
点评:本题主要考查了函数奇偶性的性质,通常将某些值根据奇偶性转化到已知的区间上进行求解,属于基础题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知函数 是
是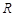 上的奇函数.当
上的奇函数.当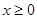 时,
时, ,则
,则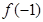 的值是 ( )
的值是 ( )
| A.3 | B.-3 | C.-1 | D.1 |
函数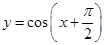 ,
,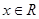 ( )
( )
| A.是偶函数 | B.是奇函数 |
| C.既不是奇函数也不是偶函数 | D.既是奇函数也是偶函数 |
函数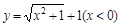 的反函数是( )
的反函数是( )
A.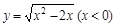 | B.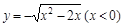 |
C.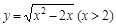 | D.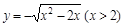 |
函数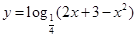 的单调递增区间是( )
的单调递增区间是( )
A.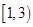 | B.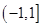 | C.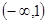 | D. |
函数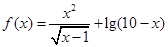 的定义域为( )
的定义域为( )
| A.R | B.[1,10] | C.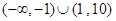 | D.(1,10) |
定义在 上的偶函数
上的偶函数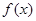 满足
满足 ,且在
,且在 上是减函数,
上是减函数, 是钝角三角形的两个锐角,则
是钝角三角形的两个锐角,则 与
与 的大小关系是
的大小关系是
A. | B. |
C. | D. |
若函数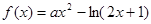 在区间
在区间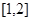 上为单调函数,则实数
上为单调函数,则实数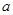 不可能取到的值为
不可能取到的值为
A.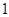 | B.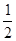 | C.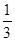 | D.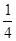 |
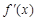 的图象如图所示,那么函数f (x)的图象最有可能的是( )
的图象如图所示,那么函数f (x)的图象最有可能的是( )