题目内容
函数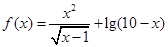 的定义域为( )
的定义域为( )
| A.R | B.[1,10] | C.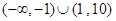 | D.(1,10) |
D
解析试题分析:要使得原式有意义,则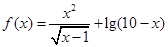 满足
满足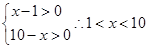 ,故可知函数的定义域为(1,10),选D.
,故可知函数的定义域为(1,10),选D.
考点:函数的定义域
点评:解决的关键是根据函数的表达式来分析函数的有意义的变量x的取值,属于基础题。

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
函数f(x)在定义域R内可导,若f(x)=f(4-x),且当x∈(-∞,2)时,(x-2)·f′(x)<0,设a=f(4),b=f(1), c=f(-1),则a,b,c由小到大排列为 ( )
| A.a<b<c | B.a<c<b | C.c<b<a | D.c<a<b |
设函数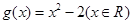 ,
,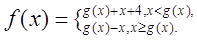 则
则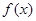 的值域是( )
的值域是( )
A.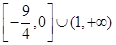 | B.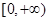 |
C.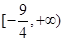 | D.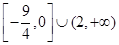 |
若函数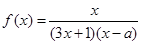 为奇函数,则
为奇函数,则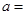 ( )
( )
| A.1 | B.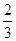 | C.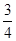 | D.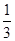 |
若函数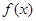 为奇函数,且当
为奇函数,且当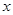 >0时
>0时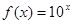 ,则
,则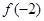 的值是( )
的值是( )
A.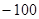 | B.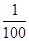  | C.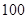 | D.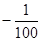 |
已知函数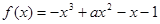 在
在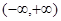 上是单调函数,则实数
上是单调函数,则实数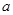 的取值范围是( )
的取值范围是( )
A.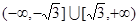 | B.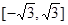 |
C.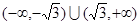 | D.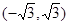 |
已知偶函数 满足当x>0时,
满足当x>0时, ,则
,则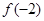 等于
等于
A.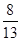 | B. | C.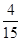 | D. |
若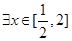 ,使
,使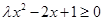 成立,则实数
成立,则实数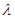 的取值范围为( )
的取值范围为( )
A.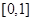 | B.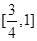 | C. | D.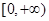 |
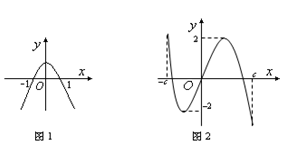
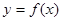 的图象如图1,函数
的图象如图1,函数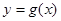 的图象如图2,则函数
的图象如图2,则函数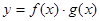 的图象大致是( )
的图象大致是( )