题目内容
2.已知log53=a,log54=b,求证:log2512=$\frac{1}{2}$(a+b)分析 直接利用对数的运算法则化简证明即可.
解答 证明:log53=a,log54=b,
log2512=$\frac{1}{2}$log512=$\frac{1}{2}$(log53+log54)=$\frac{1}{2}$(a+b).
等式成立.
点评 本题考查对数的运算法则的应用,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.设等差数列{an}满足5a7=7a10,且a1>0,Sn为其前n项和,则Sn中最大的是( )
| A. | S16 | B. | S17 | C. | S18 | D. | S16或S17 |
11.点A,B在抛物线x2=2py(p>0)上,若AB的中点是(x0,y0),当直线AB的斜率存在时,其斜率为( )
| A. | $\frac{2p}{{y}_{0}}$ | B. | $\frac{p}{{y}_{0}}$ | C. | $\frac{p}{{x}_{0}}$ | D. | $\frac{{x}_{0}}{p}$ |
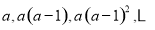 ,其前
,其前 项和为
项和为 .
. 的取值范围及
的取值范围及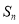 ;
;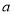 ,使
,使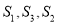 成等差数列?若存在,求出
成等差数列?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.