题目内容
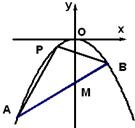
如图,抛物线的顶点O在坐标原点,焦点在y轴负半轴上.
过点M(0,-2)作直线l与抛物线相交于A,B两点,且满足
+
=(-4,-12).
(Ⅰ)求直线l和抛物线的方程;
(Ⅱ)当抛物线上一动点P从点A向点B运动时,求△ABP面积的最大值.
过点M(0,-2)作直线l与抛物线相交于A,B两点,且满足
| OA |
| OB |
(Ⅰ)求直线l和抛物线的方程;
(Ⅱ)当抛物线上一动点P从点A向点B运动时,求△ABP面积的最大值.

(Ⅰ)根据题意可设直线l的方程为y=kx-2,抛物线方程为x2=-2py(p>0) (2分)
有
得x2+2pkx-4p=0 (3分)
设点A(x1,y1),B(x2,y2)则x1+x2=-2pk,y1+y2=k(x1+x2)-4=-2pk2-4
∴
+
=(x1+x2,y1+y2)=(-2pk,-2pk2-4)(4分)
∵
+
=(-4,-12),
∴
,解得
(5分)
故直线l的方程为y=2x-2,抛物线方程为x2=-2y. (6分)
(Ⅱ)据题意,当抛物线过点P的切线与l平行时,△APB得面积最大(7分)
设点P(x0,y0),由y'=-x,故由-x0=2得x0=-2,则y0=-
=-2
∴P(-2,-2) (9分)
∴点P到直线l的距离d=
=
=
(10分)
由
,得x2+4x-4=0 (11分)
∴|AB|=
=
=4
(12分)
∴△ABP的面积的最大值为
•|AB|•d=
×4
×
=8
(14分)
有
|
设点A(x1,y1),B(x2,y2)则x1+x2=-2pk,y1+y2=k(x1+x2)-4=-2pk2-4
∴
| OA |
| OB |
∵
| OA |
| OB |
∴
|
|
故直线l的方程为y=2x-2,抛物线方程为x2=-2y. (6分)
(Ⅱ)据题意,当抛物线过点P的切线与l平行时,△APB得面积最大(7分)
设点P(x0,y0),由y'=-x,故由-x0=2得x0=-2,则y0=-
| 1 |
| 2 |
| x | 20 |
∴P(-2,-2) (9分)
∴点P到直线l的距离d=
| |2×(-2)-(-2)-2| | ||
|
| 4 | ||
|
4
| ||
| 5 |
由
|
∴|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+22 |
| (-4)2-4×(-4) |
| 10 |
∴△ABP的面积的最大值为
| 1 |
| 2 |
| 1 |
| 2 |
| 10 |
4
| ||
| 5 |
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目