题目内容
12.设函数f(x)=|2x-1|+|2x-3|(1)解不等式:f(x)≤5;
(2)若g(x)=$\frac{1}{f(x)+m}$的定义域为R,求实数m的取值范围.
分析 (1)把f(x)的解析式写成分段函数的形式,①令f(x)=5,求得x的值,可得f(x)≤5的解集.
(2)由题意可得 m≠-f(x),再根据f(x)≥2,求得m的范围.
解答 解:(1)函数f(x)=|2x-1|+|2x-3|=$\left\{\begin{array}{l}{4-4x,x<\frac{1}{2}}\\{2,\frac{1}{2}≤x≤\frac{3}{2}}\\{4x-4,x>\frac{3}{2}}\end{array}\right.$,
令f(x)=5,求得x=-$\frac{1}{4}$,或x=$\frac{9}{4}$,故f(x)≤5的解集为[-$\frac{1}{4}$,$\frac{9}{4}$].
(2)由g(x)=$\frac{1}{f(x)+m}$ 的定义域为R,可得f(x)≠-m,
即 m≠-f(x).
再根据函数f(x)的单调性可得f(x)≥2,
∴-f(x)≤-2,
故m>-2.
点评 本题主要考查带有绝对值的函数,绝对值不等式的解法,函数的值域,属于中档题.

练习册系列答案
相关题目
20.把直线x-y+1=0沿向量$\overrightarrow{a}$=(1,0)方向平移,使之与圆(x-2)2+(y-1)2=1相切,则平移的距离为( )
| A. | $\sqrt{2}-1$ | B. | $\sqrt{2}+2$ | C. | $\sqrt{2}-1$与$\sqrt{2}+1$ | D. | 2-$\sqrt{2}$与2+$\sqrt{2}$ |
1.函数f(x)=$\sqrt{{x}^{2}-(a+b)x+ab}$的定义域为M,函数g(x)=$\sqrt{x-a}$+$\sqrt{x-b}$的定义域为N(a>b>0),则下列关系式成立的是( )
| A. | M?N | B. | M?N | C. | M∩N=∅ | D. | M=N |
18.已知a>0,“x∈{-a,a}”是“|x|=a”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |
2.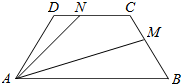 在等腰梯形ABCD中,∠A=$\frac{π}{3}$,边AB、DC的长分别为2、1,若M、N分别是边BC、CD上的点,且满足|$\frac{\overrightarrow{BM}}{\overrightarrow{BC}}$|=|$\frac{\overrightarrow{CN}}{\overrightarrow{CD}}$|,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是( )
在等腰梯形ABCD中,∠A=$\frac{π}{3}$,边AB、DC的长分别为2、1,若M、N分别是边BC、CD上的点,且满足|$\frac{\overrightarrow{BM}}{\overrightarrow{BC}}$|=|$\frac{\overrightarrow{CN}}{\overrightarrow{CD}}$|,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是( )
 在等腰梯形ABCD中,∠A=$\frac{π}{3}$,边AB、DC的长分别为2、1,若M、N分别是边BC、CD上的点,且满足|$\frac{\overrightarrow{BM}}{\overrightarrow{BC}}$|=|$\frac{\overrightarrow{CN}}{\overrightarrow{CD}}$|,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是( )
在等腰梯形ABCD中,∠A=$\frac{π}{3}$,边AB、DC的长分别为2、1,若M、N分别是边BC、CD上的点,且满足|$\frac{\overrightarrow{BM}}{\overrightarrow{BC}}$|=|$\frac{\overrightarrow{CN}}{\overrightarrow{CD}}$|,则$\overrightarrow{AM}$•$\overrightarrow{AN}$的取值范围是( )| A. | [$\frac{3}{2}$,+∞) | B. | (0,2] | C. | [$\frac{3}{2}$,3] | D. | ($\frac{3}{2}$,2) |