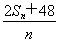Question

已知数列{an}的首项a1＝2a＋1(a是常数，且a≠－1)，

an＝2an－1＋n2－4n＋2(n≥2)，数列{bn}的首项b1＝a，

bn＝an＋n2(n≥2)．

(1)证明：{bn}从第2项起是以2为公比的等比数列；

(2)设Sn为数列{bn}的前n项和，且{Sn}是等比数列，求实数a的值；

(3)当a>0时，求数列{an}的最小项．

 

Answer 1

（1）见解析（2）a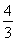＝－（3）当a∈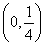时，最小项为8a－1；当a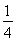＝时，最小项为4a或8a－1；当a∈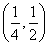时，最小项为4a；当a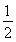＝时，最小项为4a或2a＋1；

当a∈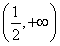时，最小项为2a＋1.

【解析】(1)证明：∵bn＝an＋n2，∴bn＋1＝an＋1＋(n＋1)2＝2an＋(n＋1)2－4(n＋1)＋2＋(n＋1)2＝2an＋2n2＝2bn(n≥2)．

由a1＝2a＋1，得a2＝4a，b2＝a2＋4＝4a＋4，∵a≠－1，

∴b2≠0，即{bn}从第2项起是以2为公比的等比数列．

(2)【解析】
由(1)知bn＝

Sn＝a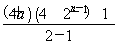＋＝－3a－4＋(2a＋2)2n，当n≥2时，

＝.

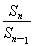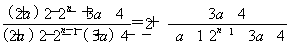∵{Sn}是等比数列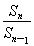，∴ (n≥2)是常数，∴3a＋4＝0，即a＝－.

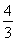(3)【解析】
由(1)知当n≥2时，bn＝(4a＋4)2n－2＝(a＋1)2n，

∴an＝

∴数列{an}为2a＋1，4a，8a－1，16a，32a＋7，…

显然最小项是前三项中的一项．

当a∈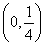时，最小项为8a－1；当a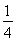＝时，最小项为4a或8a－1；

当a∈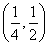时，最小项为4a；当a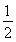＝时，最小项为4a或2a＋1；

当a∈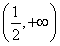时，最小项为2a＋1.