题目内容
设F为抛物线y=-
x2的焦点,该抛物线在点P(-4,-4)处的切线l与x轴的交点为Q,则△PFQ的外接圆的方程为
| 1 |
| 4 |
(x+2)2+(y+
)2=
| 5 |
| 2 |
| 25 |
| 4 |
(x+2)2+(y+
)2=
.| 5 |
| 2 |
| 25 |
| 4 |
分析:确定抛物线的焦点与在点P(-4,-4)处的切线,求出Q的坐标,再利用PQ⊥QF,即可求得△PFQ的外接圆的方程.
解答:解:抛物线y=-
x2的焦点F(0,-1)
求导函数可得y′=-
x,当x=-4时,y′=-
× (-4)=2
∴抛物线在点P(-4,-4)处的切线为y+4=2(x+4),即2x-y+4=0
令y=0,可得x=-2,∴Q(-2,0)
∵kQF=
=-
,kPQ=2
∴PQ⊥QF
∴△PFQ的外接圆的直径为PF
∵P(-4,-4)、F(0,-1)
∴圆心坐标为(-2,-
),半径为
∴△PFQ的外接圆的方程为(x+2)2+(y+
)2=
故答案为:(x+2)2+(y+
)2=
| 1 |
| 4 |
求导函数可得y′=-
| 1 |
| 2 |
| 1 |
| 2 |
∴抛物线在点P(-4,-4)处的切线为y+4=2(x+4),即2x-y+4=0
令y=0,可得x=-2,∴Q(-2,0)
∵kQF=
| -1 |
| 2 |
| 1 |
| 2 |
∴PQ⊥QF
∴△PFQ的外接圆的直径为PF
∵P(-4,-4)、F(0,-1)
∴圆心坐标为(-2,-
| 5 |
| 2 |
| 5 |
| 2 |
∴△PFQ的外接圆的方程为(x+2)2+(y+
| 5 |
| 2 |
| 25 |
| 4 |
故答案为:(x+2)2+(y+
| 5 |
| 2 |
| 25 |
| 4 |
点评:本题考查抛物线的性质与切线,考查三角形的外接圆,解题的关键是求出抛物线的切线,确定三角形三个顶点的坐标.

练习册系列答案
相关题目
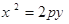
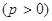 的焦点,A、B、C为该抛物线上三点,已知
的焦点,A、B、C为该抛物线上三点,已知 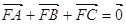 且
且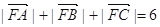 .
.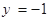 相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。