题目内容
设F为抛物线E: 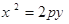
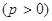 的焦点,A、B、C为该抛物线上三点,已知
的焦点,A、B、C为该抛物线上三点,已知 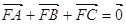 且
且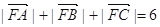 .
.
(1)求抛物线方程;
(2)设动直线l与抛物线E相切于点P,与直线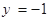 相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
相交于点Q。证明以PQ为直径的圆恒过y轴上某定点。
【答案】
(1) (2)本题主要由
(2)本题主要由 ·
·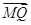 =0来求出M点。
=0来求出M点。
【解析】
试题分析:解;(1)由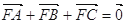 知
知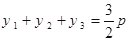 又
又
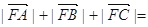
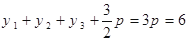 所以
所以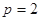 所以所求抛物线方程为
所以所求抛物线方程为
(2)设点P(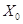 ,
,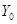 ),
),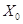 ≠0.∵Y=
≠0.∵Y=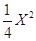 ,
,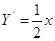 ,
,
切线方程:y-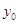 =
=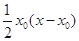 ,即y=
,即y=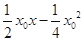
由
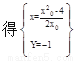 ∴Q(
∴Q(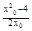 ,-1)
,-1)
设M(0,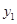 )∴
)∴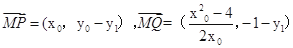 ,∵
,∵ ·
·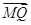 =0
=0
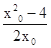 -
-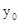 -
-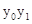 +
+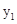 +
+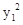 =0,又
=0,又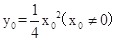 ,∴联立解得
,∴联立解得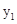 =1
=1
故以PQ为直径的圆过y轴上的定点M(0,1)
考点:抛物线的方程
点评:关于曲线的大题,第一问一般是求出曲线的方程,第二问常与直线结合起来,当涉及到交点时,常用到根与系数的关系式: (
(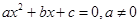 )。
)。

练习册系列答案
相关题目
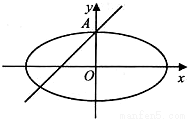
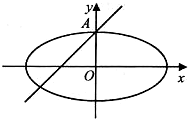 如图所示,椭圆
如图所示,椭圆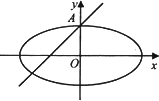
 的离心率为
的离心率为 ,且A(0,2)是椭圆C的顶点.
,且A(0,2)是椭圆C的顶点.
 的离心率为
的离心率为 ,且A(0,2)是椭圆C的顶点.
,且A(0,2)是椭圆C的顶点.