题目内容
【题目】已知椭圆
的左、右焦点分别为
， 
，直线
交椭圆
于
， 
两点， 
的周长为16， 
的周长为12.
（1）求椭圆
的标准方程与离心率；
（2）若直线
与椭圆
交于
两点，且
是线段
的中点，求直线
的一般方程.
【答案】(1) 椭圆E的标准方程为
，离心率
(2) 
【解析】试题分析：（1）由直线
交椭圆
于
， 
两点， 
的周长为16， 
的周长为12，可得
， 
，再结合
，即可求出
， 
， 
的值，从而求出椭圆
的标准方程与离心率；（2）由（1）知
，易知直线
的斜率存在，设为
，设
，利用点差法，即可求出
，从而求出直线
的一般方程.
试题解析：（1）由题知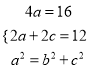
，解得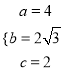
∴椭圆E的标准方程为
，离心率
.
（2）由（1）知
，
易知直线
的斜率存在，设为
，设
,则
， 
∴
，
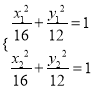又
是线段CD的中点
∴
，
故直线
的方程为
，化为一般形式即： 
.
练习册系列答案
相关题目
【题目】(2016·辽宁五校联考)某车间加工零件的数量x与加工时间y的统计数据如表：
零件数x(个) | 10 | 20 | 30 |
加工时间y(分钟) | 21 | 30 | 39 |
现已求得上表数据的线性回归方程
＝
＋
中的
值为0.9，则据此回归模型可以预测，加工100个零件所需要的加工时间约为( )
A. 84分钟 B. 94分钟
C. 102分钟 D. 112分钟
