题目内容
已知两点B(6,0)和C(-6,0),设点A与B、C的连线AB、AC的斜率分别为k1,k2,如果k1k2=
,那么点A的轨迹一定不是下列曲线(或其一部分)( )
| 1 |
| m |
分析:根据直线AB,AC的斜率分别是k1,k2,且k1•k2=
,建立方程,化简即可得到动点A的轨迹的方程.
| 1 |
| m |
解答:解:设A(x,y),由题意得,
•
=
(x≠±6),
即x2-my2-36=0.
所以点A的轨迹的方程为 x2-my2=36(x≠±6),
当m>0且m≠1时,表示椭圆.
当m=1时,表示圆.
当m<0时,表示双曲线.
那么点A的轨迹一定不是抛物线.
故选D.
| y |
| x-6 |
| y |
| x+6 |
| 1 |
| m |
即x2-my2-36=0.
所以点A的轨迹的方程为 x2-my2=36(x≠±6),
当m>0且m≠1时,表示椭圆.
当m=1时,表示圆.
当m<0时,表示双曲线.
那么点A的轨迹一定不是抛物线.
故选D.
点评:本题考查轨迹方程,考查圆锥曲线的方程,考查分类讨论思想,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
已知两点A(-6,0),B(6,8),P是线段AB上一点,且有AP:PB=3:5,则点P到直线3x+4y-18=0的距离是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
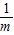 ,那么点A的轨迹一定不是下列曲线(或其一部分)( )
,那么点A的轨迹一定不是下列曲线(或其一部分)( )