题目内容
(本小题13分)在平面直角坐标系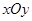 中,
中,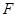 是抛物线
是抛物线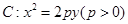 的焦点,
的焦点,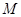 是抛物线
是抛物线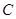 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过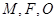 三点的圆的圆心为
三点的圆的圆心为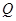 ,点
,点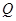 到抛物线
到抛物线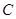 的准线的距离为
的准线的距离为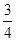 .
.
(Ⅰ)求抛物线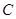 的方程;
的方程;
(Ⅱ)是否存在点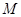 ,使得直线
,使得直线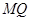 与抛物线
与抛物线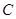 相切于点
相切于点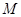 ?若存在,求出点
?若存在,求出点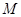 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
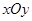 中,
中,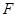 是抛物线
是抛物线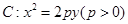 的焦点,
的焦点,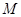 是抛物线
是抛物线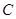 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过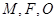 三点的圆的圆心为
三点的圆的圆心为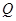 ,点
,点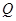 到抛物线
到抛物线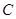 的准线的距离为
的准线的距离为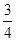 .
.(Ⅰ)求抛物线
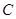 的方程;
的方程;(Ⅱ)是否存在点
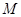 ,使得直线
,使得直线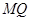 与抛物线
与抛物线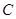 相切于点
相切于点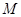 ?若存在,求出点
?若存在,求出点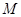 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;(Ⅰ) 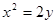 (Ⅱ)
(Ⅱ) 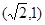
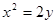 (Ⅱ)
(Ⅱ) 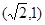
试题分析:(Ⅰ)F抛物线C:x2=2py(p>0)的焦点F
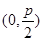 ,设M
,设M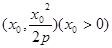 ,
,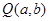 ,由题意可知
,由题意可知 ,则点Q到抛物线C的准线的距离为
,则点Q到抛物线C的准线的距离为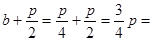
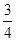 ,解得
,解得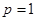 ,于是抛物线C的方程为
,于是抛物线C的方程为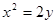 . 5分
. 5分(Ⅱ)假设存在点M,使得直线MQ与抛物线C相切于点M,
而
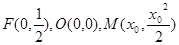 ,
,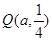 ,
,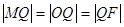 ,
,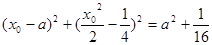 ,
,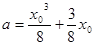 ,
,由
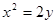 可得
可得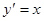 ,
,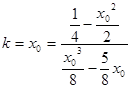 ,则
,则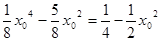 ,
,即
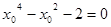 ,而
,而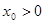 ,解得
,解得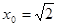 ,点M的坐标为
,点M的坐标为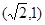 . 13分
. 13分点评:第二问属于探索性题目,此类题目的求解思路是假设满足条件的点存在,然后按已知条件去求解计算该点,若能算出则点存在,否则点不存在,另曲线在某一点处的切线斜率转化为该点处导数。此题有一定的综合性

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
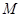 ,两个焦点为
,两个焦点为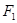 、
、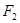 ,
,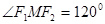 ,则双曲线的离心率为____________.
,则双曲线的离心率为____________.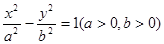 的离心率为2,则双曲线
的离心率为2,则双曲线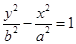 的离心率为( )
的离心率为( )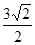
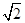
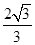
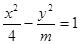 的离心率为半径,右焦点为圆心的圆与双曲线的渐近线相切,则
的离心率为半径,右焦点为圆心的圆与双曲线的渐近线相切,则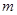 的值为( )
的值为( )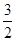

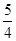
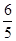
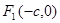 、
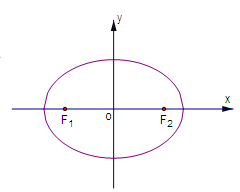
、 分别是椭圆
分别是椭圆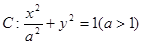 的左、右焦点,
的左、右焦点,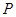 为椭圆
为椭圆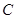 上任意一点,且
上任意一点,且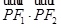 最小值为
最小值为 .
.
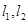 均与椭圆
均与椭圆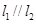 ,试探究在
,试探究在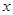 轴上是否存在定点
轴上是否存在定点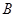 ,点
,点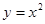 上有一条长为2的动弦AB,则AB中点M到x轴的最短距离为
上有一条长为2的动弦AB,则AB中点M到x轴的最短距离为 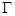 的方程为
的方程为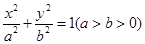 ,点P的坐标为(-a,b).
,点P的坐标为(-a,b).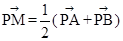 ,求点
,求点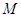 的坐标;
的坐标;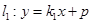 交椭圆
交椭圆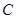 、
、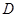 两点,交直线
两点,交直线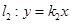 于点
于点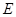 .若
.若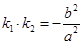 ,证明:
,证明: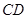 的中点;
的中点;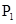 、
、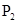 满足
满足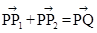 ,写出求作点
,写出求作点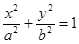 (a>b>0)的右焦点为F
(a>b>0)的右焦点为F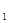 (1,0),离心率为
(1,0),离心率为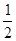 ,P为左顶点。
,P为左顶点。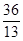 ,求直线AB的方程。
,求直线AB的方程。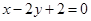 经过椭圆
经过椭圆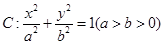 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆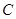 的右顶点为
的右顶点为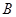 ,点
,点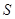 和椭圆
和椭圆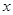 轴上方的动点,直线,
轴上方的动点,直线,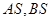 与直线
与直线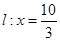 分别交于
分别交于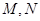 两点。
两点。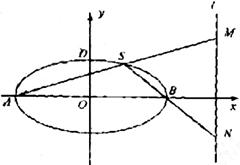
 ,使得
,使得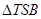 的面积为
的面积为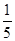 ?若存在,确定点
?若存在,确定点