题目内容
已知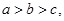
求证：
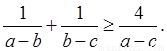
【解析】本试题组要是利用均值不等式配凑法，来证明关于不等式的证明问题。也可以运用分析法得到。
【答案】
证明：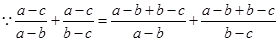
，
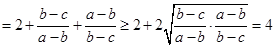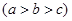
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
已知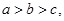 求证：
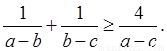
【解析】本试题组要是利用均值不等式配凑法，来证明关于不等式的证明问题。也可以运用分析法得到。
证明：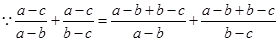
，
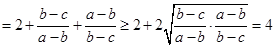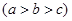
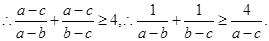
名校课堂系列答案
∵AB=AC
∴
中，
为
边上的中线，
为
上任意一点，
交
.求证：
． 
，然后利用平行性得到相似比，
，
，然后得到比例相等。充分利用比值问题转化得到结论。
作
，∴
， 
， ∵
，
，
，
，即
满足
且对一切
,
，然后得到
，从而求证
。
，可得数列的通项公式。
然后利用累加法思想求证得到证明。
，求证：
.