题目内容
已知数列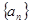 满足
满足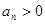 且对一切
且对一切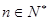 ,
,
有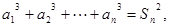
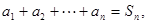
(Ⅰ)求证:对一切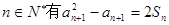
(Ⅱ)求数列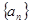 通项公式.
通项公式.
(Ⅲ)求证: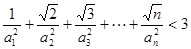
【解析】第一问利用,已知表达式,可以得到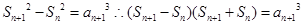 ,然后得到
,然后得到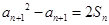 ,从而求证
。
,从而求证
。
第二问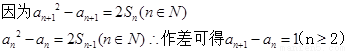 ,可得数列的通项公式。
,可得数列的通项公式。
第三问中,利用放缩法的思想,我们可以得到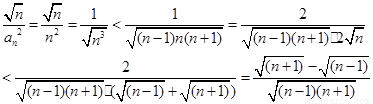
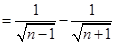 然后利用累加法思想求证得到证明。
然后利用累加法思想求证得到证明。
解: (1) 证明:
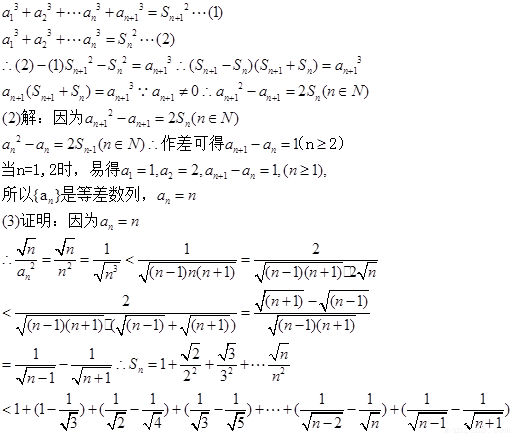
【答案】
见解析

练习册系列答案
相关题目
题目内容
已知数列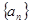 满足
满足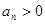 且对一切
且对一切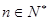 ,
,
有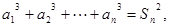
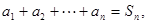
(Ⅰ)求证:对一切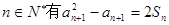
(Ⅱ)求数列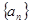 通项公式.
通项公式.
(Ⅲ)求证: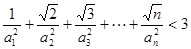
【解析】第一问利用,已知表达式,可以得到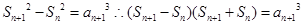 ,然后得到
,然后得到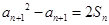 ,从而求证
。
,从而求证
。
第二问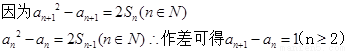 ,可得数列的通项公式。
,可得数列的通项公式。
第三问中,利用放缩法的思想,我们可以得到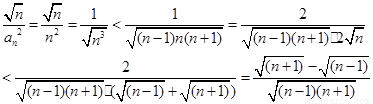
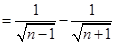 然后利用累加法思想求证得到证明。
然后利用累加法思想求证得到证明。
解: (1) 证明:
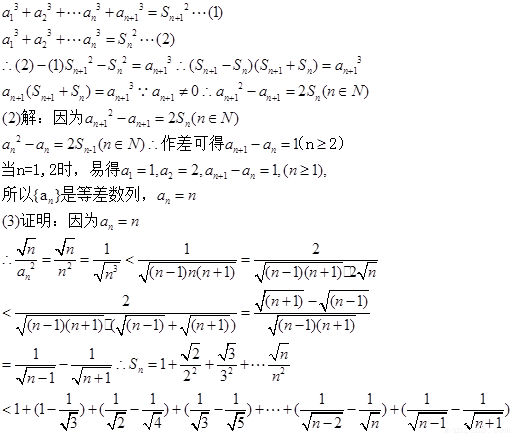
见解析
