题目内容
已知公差大于零的等差数列 的前n项和为
的前n项和为 ,且满足:
,且满足: ,
, .
.
(1)求数列 的通项公式
的通项公式 ;
;
(2)若数列 是等差数列,且
是等差数列,且 ,求非零常数c;
,求非零常数c;
(3)在(2)的条件下,设 ,已知数列
,已知数列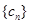 为递增数列,求实数
为递增数列,求实数 的取值范围.
的取值范围.
 的前n项和为
的前n项和为 ,且满足:
,且满足: ,
, .
.(1)求数列
 的通项公式
的通项公式 ;
;(2)若数列
 是等差数列,且
是等差数列,且 ,求非零常数c;
,求非零常数c;(3)在(2)的条件下,设
 ,已知数列
,已知数列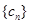 为递增数列,求实数
为递增数列,求实数 的取值范围.
的取值范围.(1)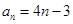 (2)
(2)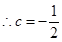 (3)
(3)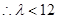
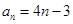 (2)
(2)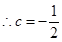 (3)
(3)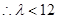
试题分析:解:(1)由
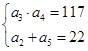 得,
得,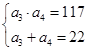
解得
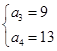 或
或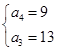
因为等差数列
 的公差大于零,所以
的公差大于零,所以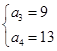
由
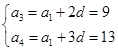 解得
解得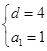
所以
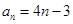
(2)由(1)得:
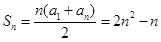
所以
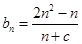
由
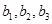 成等差数列得
成等差数列得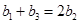
列示得
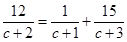 ,解得
,解得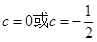
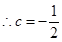
(3)
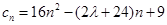 ,由
,由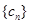 为递增数列,得
为递增数列,得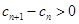
得
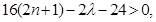 分离参数得
分离参数得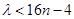 ,又
,又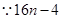 在n=1时取得最小值12
在n=1时取得最小值12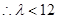
点评:在等差数列中,当涉及到两项相加(像
 ),常用到性质:
),常用到性质: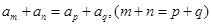
,而在等比数列中,若涉及到两项相乘,则常用到性质:
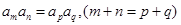 。另外,数列的定义很重要,像本题第二小题就用到等差数列的定义,结合数列的定义还可以证明一个数列是什么数列。
。另外,数列的定义很重要,像本题第二小题就用到等差数列的定义,结合数列的定义还可以证明一个数列是什么数列。
练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
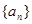 的公差
的公差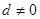 ,等比数列
,等比数列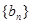 公比为
公比为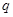 ,且
,且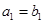 ,
,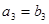 ,
,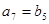
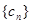 ,是否存在正整数
,是否存在正整数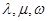 (其中
(其中 )使得
)使得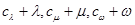 都构成等差数列?若存在,求出一组
都构成等差数列?若存在,求出一组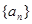 中,al =" l," a2 =" 2+3" , a3 =" 4+5+6" , a4 =" 7+8+9+10" , ……,则a10的值是_______
中,al =" l," a2 =" 2+3" , a3 =" 4+5+6" , a4 =" 7+8+9+10" , ……,则a10的值是_______ 满足
满足 .
. ,并由此猜想
,并由此猜想 的一个通项公式,证明你的结论;
的一个通项公式,证明你的结论; ,不等式
,不等式 对一切
对一切 都成立,求正整数m的最大值。
都成立,求正整数m的最大值。 的第 项.
的第 项. 满足
满足 ,
, ,则它的前10项的和
,则它的前10项的和 _____
_____ 中,
中, 的对边分别是
的对边分别是 ,且
,且 是
是 的等差中项,则角
的等差中项,则角 = .
= . 的公差为
的公差为 ,若其前13项和
,若其前13项和 ,则
,则 ( )
( ) 是等差数列,对于
是等差数列,对于 ,则数列
,则数列 也是等差数列。类比上述性质,若数列
也是等差数列。类比上述性质,若数列 是各项都为正数的等比数列,对于
是各项都为正数的等比数列,对于 ,则
,则 时,数列
时,数列 也是等比数列。
也是等比数列。