题目内容
如图,已知椭圆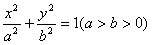 的长轴为AB,过点B的直线l与x轴垂直,直线(2-k)x-(1+2k)y+(1+2k)=0(k∈R)所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
的长轴为AB,过点B的直线l与x轴垂直,直线(2-k)x-(1+2k)y+(1+2k)=0(k∈R)所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率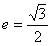 ,
,
(1)求椭圆的标准方程;
(2)设P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连接AQ并延长交直线l于点M,N为MB的中点,试判断直线QN与以AB为直径的圆O的位置关系。
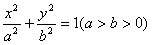 的长轴为AB,过点B的直线l与x轴垂直,直线(2-k)x-(1+2k)y+(1+2k)=0(k∈R)所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
的长轴为AB,过点B的直线l与x轴垂直,直线(2-k)x-(1+2k)y+(1+2k)=0(k∈R)所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率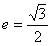 ,
,(1)求椭圆的标准方程;
(2)设P是椭圆上异于A、B的任意一点,PH⊥x轴,H为垂足,延长HP到点Q使得HP=PQ,连接AQ并延长交直线l于点M,N为MB的中点,试判断直线QN与以AB为直径的圆O的位置关系。

解:(1)将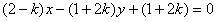
整理得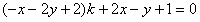 ,
,
解方程组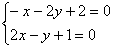 得直线所经过的定点为(0,1),
得直线所经过的定点为(0,1),
∴b=1,
由离心率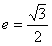 ,得a=2,
,得a=2,
∴椭圆的标准方程为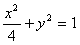 ;
;
(2)设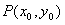 ,则
,则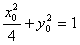 ,
,
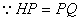 ,
,
∴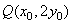 ,
,
∴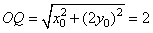 ,
,
∴Q点在以O为圆心,2为半径的圆上,即Q点在以AB为直径的圆O上。又A(-2,0),∴直线l的方程为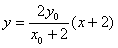 ,
,
令x=2,得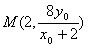 。
。
又B(2,0),N为MB的中点,
∴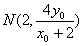 ,
,
∴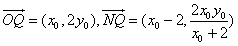 ,
,
∴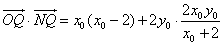
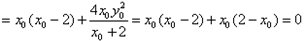 ,
,
∴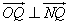 ,
,
∴直线QN与以AB为直径的圆O相切。
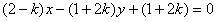
整理得
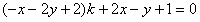 ,
,解方程组
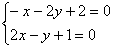 得直线所经过的定点为(0,1),
得直线所经过的定点为(0,1),∴b=1,
由离心率
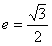 ,得a=2,
,得a=2,∴椭圆的标准方程为
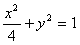 ;
;(2)设
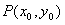 ,则
,则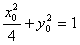 ,
,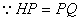 ,
,∴
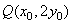 ,
,∴
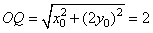 ,
,∴Q点在以O为圆心,2为半径的圆上,即Q点在以AB为直径的圆O上。又A(-2,0),∴直线l的方程为
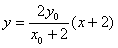 ,
,令x=2,得
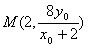 。
。又B(2,0),N为MB的中点,
∴
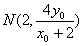 ,
,∴
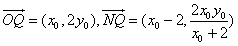 ,
,∴
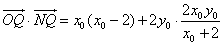
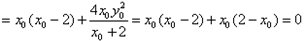 ,
,∴
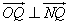 ,
,∴直线QN与以AB为直径的圆O相切。

练习册系列答案
相关题目
 (2003•北京)如图,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0
(2003•北京)如图,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0

 的长轴为
的长轴为 ,过点
,过点 的直线
的直线 与
与 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率

 是椭圆上异于
是椭圆上异于 、
、 轴,
轴, 为垂足,延长
为垂足,延长 到点
到点 使得
使得 ,连接
,连接 并延长交直线
并延长交直线 ,
, 为
为 的中点.试判断直线
的中点.试判断直线 与以
与以 的位置关系.
的位置关系. 的长轴为
的长轴为 ,过点
,过点 的直线
的直线 与
与 轴垂直,直线
轴垂直,直线 所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
所经过的定点恰好是椭圆的一个顶点,且椭圆的离心率
 是椭圆上异于
是椭圆上异于 、
、 轴,
轴, 为垂足,延长
为垂足,延长 到点
到点 使得
使得 ,连接
,连接 并延长交直线
并延长交直线 ,
, 为
为 的中点.试判断直线
的中点.试判断直线 与以
与以 的位置关系.
的位置关系.