Question

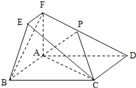
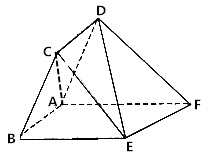
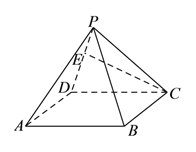
【题目】如图， 为正四棱锥侧棱上异于， 的一点，给出下列结论：

①侧面可以是正三角形．

②侧面可以是直角三角形．

③侧面上存在直线与平行．

④侧面上存在直线与垂直．

其中，所有正确结论的序号是__________．

Answer 1

【答案】①④

【解析】为正四棱锥侧棱上异于， 的一点，知：
在①中，当侧棱与底面边长相等时，侧面是正三角形，故①正确；
在②中，∵正四棱锥中 ，
∴当侧面是直角三角形时， 不成立，
故侧面不可以是直角三角形，故②错误；
在③中，若侧面上存在直线与平行，则与点一定重合，
与为正四棱锥侧棱上异于， 的一点矛盾，
故侧面上不存在直线与平行，故③错误；
在④中，侧面上一定存在直线与垂直，故④正确．
故选①④．

【点睛 】本题考查命题真假的判断，解题时要认真审题，注意空间中线线、线面、面面间的益关系的合理运用．