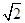题目内容
双曲线 的焦点坐标是( )
的焦点坐标是( )
A. | B. | C. | D. |
C
解析试题分析:因为双曲线方程为 ,因此可知
,因此可知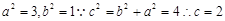
故其有两个焦点,分别是 ,因此选C.
,因此选C.
考点:本题主要是考查双曲线的几何性质的运用。
点评:解决该试题的关键是理解双曲线中a,b表示的值,以及a,b,c的关系的运用。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若抛物线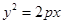 的焦点与椭圆
的焦点与椭圆 的右焦点重合,则
的右焦点重合,则 的值为( )
的值为( )
| A.-2 | B.2 | C.-4 | D.4 |
与椭圆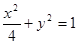 共焦点且过点
共焦点且过点 的双曲线方程是( )
的双曲线方程是( )
A.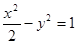 | B.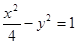 |
C. | D. |
等轴双曲线C的中心在原点,焦点在 轴上,C与抛物线
轴上,C与抛物线 的准线交于A,B两点,
的准线交于A,B两点, ,则C的实轴长为( )
,则C的实轴长为( )
| A.2 | B. | C.4 | D. |
直线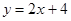 与抛物线
与抛物线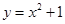 所围成封闭图形的面积是( )
所围成封闭图形的面积是( )
A.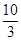 | B.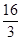 | C.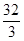 | D.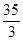 |
直线 与曲线
与曲线 相切于点
相切于点 ,则
,则 的值为 ( )
的值为 ( )
| A.-3 | B.9 |
| C.-15 | D.-7 |
已知椭圆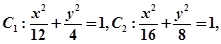 则 ( )
则 ( )
A.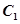 与 与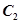 顶点相同. 顶点相同. | B.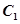 与 与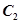 长轴长相同. 长轴长相同. |
C.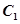 与 与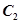 短轴长相同. 短轴长相同. | D.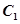 与 与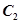 焦距相等. 焦距相等. |
椭圆 上的一点
上的一点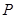 ,它到椭圆的一个焦点
,它到椭圆的一个焦点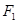 的距离是7,则它到另一个焦点
的距离是7,则它到另一个焦点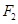 的距离是( )
的距离是( )
A.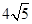 | B.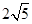 | C.12 | D.5 |