题目内容
已知两个向量集合M={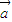 |
|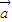 =(cosα,
=(cosα,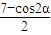 ),α∈R},N={
),α∈R},N={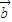 |
|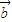 =(cosβ,λ+sinβ),β∈R},若M∩N≠∅,则λ的取值范围是( )
=(cosβ,λ+sinβ),β∈R},若M∩N≠∅,则λ的取值范围是( )A.(-3,5]
B.[
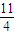 ,5]
,5]C.[2,5]
D.[5,+∞)
【答案】分析:M∩N≠Φ,即是说方程组 有解,两式消去α得出3+sin2β=λ+sinβ后,移向得出λ=sin2β-sinβ-3=(sinβ-
有解,两式消去α得出3+sin2β=λ+sinβ后,移向得出λ=sin2β-sinβ-3=(sinβ- )2+
)2+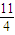 .根据sinβ的有界性求出λ的取值范围.
.根据sinβ的有界性求出λ的取值范围.
解答:解:M∩N≠Φ,即是说方程组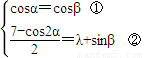 有解.
有解.
而 =
=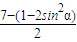 =3+sin2α,②即为3+sin2α=λ+sinβ③
=3+sin2α,②即为3+sin2α=λ+sinβ③
由①得sin2α=sin2β,代入③消去α得3+sin2β=λ+sinβ,移向得出λ=sin2β-sinβ-3=(sinβ- )2+
)2+ .
.
∵sinβ∈[-1,1],∴当sinβ= 时,λ的最小值为
时,λ的最小值为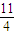 ,当sinβ=-1时,λ的最大值为5.
,当sinβ=-1时,λ的最大值为5.
点评:本题考查方程思想、函数思想、分离参数的思想方法.考查分析、解决、逻辑思维、计算能力.
 有解,两式消去α得出3+sin2β=λ+sinβ后,移向得出λ=sin2β-sinβ-3=(sinβ-
有解,两式消去α得出3+sin2β=λ+sinβ后,移向得出λ=sin2β-sinβ-3=(sinβ- )2+
)2+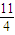 .根据sinβ的有界性求出λ的取值范围.
.根据sinβ的有界性求出λ的取值范围.解答:解:M∩N≠Φ,即是说方程组
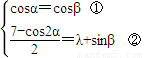 有解.
有解.而
 =
=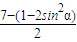 =3+sin2α,②即为3+sin2α=λ+sinβ③
=3+sin2α,②即为3+sin2α=λ+sinβ③由①得sin2α=sin2β,代入③消去α得3+sin2β=λ+sinβ,移向得出λ=sin2β-sinβ-3=(sinβ-
 )2+
)2+ .
.∵sinβ∈[-1,1],∴当sinβ=
 时,λ的最小值为
时,λ的最小值为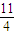 ,当sinβ=-1时,λ的最大值为5.
,当sinβ=-1时,λ的最大值为5.点评:本题考查方程思想、函数思想、分离参数的思想方法.考查分析、解决、逻辑思维、计算能力.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
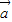 |
|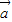 =(cosα,
=(cosα,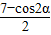 ),α∈R},N={
),α∈R},N={ |
|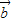 =(cosβ,λ+sinβ),β∈R},若M∩N≠∅,则λ的取值范围是( )
=(cosβ,λ+sinβ),β∈R},若M∩N≠∅,则λ的取值范围是( )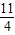 ,5]
,5]