题目内容
已知两个向量集合M={| a |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| b |
分析:由已知中两个向量集合M={
|
=(
-t,
+t),t∈R},N={
|
=(cosα,λ+sinα),α∈R},M∩N是只有一个元素的集合,我们易得关于t的方程组
只有一个解,利用三角函数平方关系,易得2t2-2λt+(λ2-λ-
)=0只有一个解,根据二次方程根的个数与△的关系,即可得到满足条件的△的值.
| a |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
| b |
| b |
|
| 1 |
| 2 |
解答:解:∵集合M={
|
=(
-t,
+t),t∈R},
N={
|
=(cosα,λ+sinα),α∈R},
若M∩N是只有一个元素的集合,
则
只有一个解
即方程(
-t)2+(
+t-λ)2=1只有一个解
即2t2-2λt+(λ2-λ-
)=0只有一个解
故△=4λ2-8(λ2-λ-
)=0
解得λ=1±
故答案为:1±
| a |
| a |
| 1 |
| 2 |
| 1 |
| 2 |
N={
| b |
| b |
若M∩N是只有一个元素的集合,
则
|
即方程(
| 1 |
| 2 |
| 1 |
| 2 |
即2t2-2λt+(λ2-λ-
| 1 |
| 2 |
故△=4λ2-8(λ2-λ-
| 1 |
| 2 |
解得λ=1±
| 2 |
故答案为:1±
| 2 |
点评:本题考查的知识点是相等向量与相反向量,其中根据向量相等结合已知条件构造关于t的方程组是解答本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
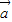 |
|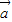 =(cosα,
=(cosα,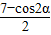 ),α∈R},N={
),α∈R},N={ |
|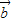 =(cosβ,λ+sinβ),β∈R},若M∩N≠∅,则λ的取值范围是( )
=(cosβ,λ+sinβ),β∈R},若M∩N≠∅,则λ的取值范围是( )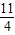 ,5]
,5]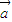 |
|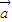 =(cosα,
=(cosα,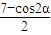 ),α∈R},N={
),α∈R},N={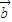 |
|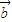 =(cosβ,λ+sinβ),β∈R},若M∩N≠∅,则λ的取值范围是( )
=(cosβ,λ+sinβ),β∈R},若M∩N≠∅,则λ的取值范围是( )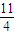 ,5]
,5]