题目内容
已知函数f(x)＝|x2＋2x－1|，若a＜b＜－1，且f(a)＝f(b)，则ab＋a＋b的取值范围是________．
(－1,1)
【解析】作出函数图象可知若a＜b＜－1，且f(a)＝f(b)，即为a2＋2a－1＝－(b2＋2b－1)，
整理得(a＋1)2＋(b＋1)2＝4，设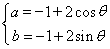
θ∈
∪
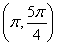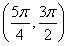，所以ab＋a＋b＝－1＋2sin 2θ∈(－1,1)．
练习册系列答案
相关题目
题目内容
已知函数f(x)＝|x2＋2x－1|，若a＜b＜－1，且f(a)＝f(b)，则ab＋a＋b的取值范围是________．
(－1,1)
【解析】作出函数图象可知若a＜b＜－1，且f(a)＝f(b)，即为a2＋2a－1＝－(b2＋2b－1)，
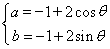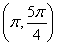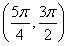整理得(a＋1)2＋(b＋1)2＝4，设θ∈∪，所以ab＋a＋b＝－1＋2sin 2θ∈(－1,1)．
