题目内容
已知函数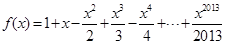 ,
,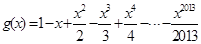 ,设函数
,设函数
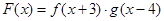 ,且函数
,且函数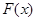 的零点均在区间
的零点均在区间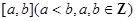 内,则
内,则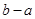 的最小值为
的最小值为
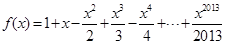 ,
,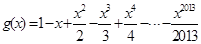 ,设函数
,设函数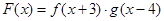 ,且函数
,且函数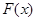 的零点均在区间
的零点均在区间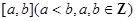 内,则
内,则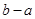 的最小值为
的最小值为A.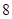 | B.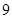 | C.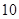 | D.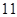 |
C
由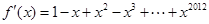 ,
,
可得当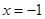 时
时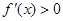 ,
,
当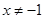 时
时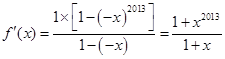 ,
,
若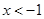 则
则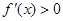 ,若
,若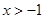 则
则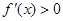 .
.
综上可知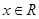 时,
时,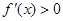 ,故
,故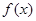 在
在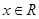 上为增函数,
上为增函数,
又因为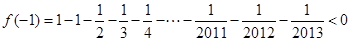 ,
,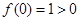 ,
,
所以函数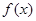 在其定义域内的区间(-1,0)上只有一个零点.
在其定义域内的区间(-1,0)上只有一个零点.
同理可证明g(x)在R上是减函数,由于g(1)<0,g(2)>0,所以g(x)在区间(1,2)上有一个零点,
所以F(x)在区间(-4,-3)或(5,6)上有零点,由于F(x)的零点在区间[a,b]上,所以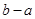 的最小值为
的最小值为
6-(-4)=10.
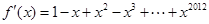 ,
,可得当
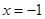 时
时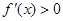 ,
,当
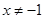 时
时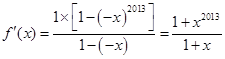 ,
,若
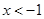 则
则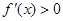 ,若
,若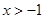 则
则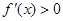 .
.综上可知
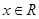 时,
时,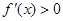 ,故
,故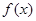 在
在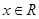 上为增函数,
上为增函数,又因为
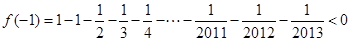 ,
,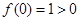 ,
,所以函数
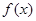 在其定义域内的区间(-1,0)上只有一个零点.
在其定义域内的区间(-1,0)上只有一个零点.同理可证明g(x)在R上是减函数,由于g(1)<0,g(2)>0,所以g(x)在区间(1,2)上有一个零点,
所以F(x)在区间(-4,-3)或(5,6)上有零点,由于F(x)的零点在区间[a,b]上,所以
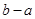 的最小值为
的最小值为6-(-4)=10.

练习册系列答案
相关题目
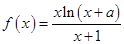
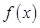 在
在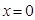 处取到极值,求
处取到极值,求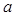 的值.
的值.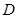 上的函数
上的函数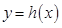 在点
在点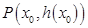 处的切线方程为
处的切线方程为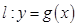 ,若
,若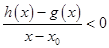 在
在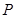 为函数的
为函数的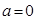 时,试问函数
时,试问函数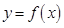 是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.
是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.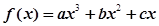 在
在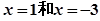 处取得极值,且
处取得极值,且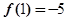
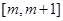 上单调递增,求
上单调递增,求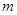 的取值范围
的取值范围 .
.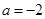 时,求函数
时,求函数 的单调区间;
的单调区间; ,使得函数
,使得函数 ?若存在,,求
?若存在,,求 ,总有
,总有 ,则称
,则称 是
是 的凸
的凸 ,则称
,则称 时,利用定义分析
时,利用定义分析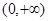 上为增函数的是 ( )
上为增函数的是 ( )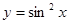
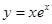
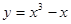
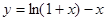
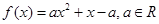 。
。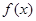 有最大值
有最大值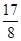 ,求实数
,求实数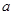 的值;
的值;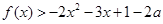 对一切实数
对一切实数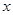 恒成立,求实数
恒成立,求实数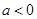 ,解不等式
,解不等式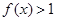 。
。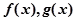 都是定义在
都是定义在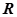 上的函数,并满足:(1)
上的函数,并满足:(1)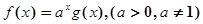 ;
;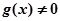 ;(3)
;(3)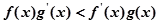 且
且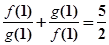 ,则
,则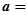 ( )
( )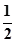
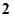
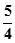
 在
在 上为减函数,则
上为减函数,则 的取值范围是 .
的取值范围是 . 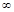 )
)