题目内容
15.若一次函数y=f(x)在区间[-1,2]上的最小值为1,最大值为3,则y=f(x)的解析式为f(x)=$\frac{2}{3}x+\frac{5}{3}$或f(x)=$-\frac{2}{3}x-\frac{5}{3}$.分析 设出函数的解析式,利用已知条件求出解析式即可.
解答 解:设函数的解析式为:f(x)=ax+b,一次函数y=f(x)在区间[-1,2]上的最小值为1,最大值为3,
当a>0时,$\left\{\begin{array}{l}2a+b=3\\-a+b=1\end{array}\right.$,可得a=$\frac{2}{3}$,b=$\frac{5}{3}$,
函数的解析式为:f(x)=$\frac{2}{3}x+\frac{5}{3}$.
当a<0时,$\left\{\begin{array}{l}2a+b=1\\-a+b=3\end{array}\right.$,可得a=-$\frac{2}{3}$,b=-$\frac{5}{3}$,
函数的解析式为:f(x)=$-\frac{2}{3}x-\frac{5}{3}$.
故答案为:f(x)=$\frac{2}{3}x+\frac{5}{3}$或f(x)=$-\frac{2}{3}x-\frac{5}{3}$.
点评 本题考查函数的解析式的求法,考查计算能力.

练习册系列答案
相关题目
6.若log4x=3,则log16x等于( )
| A. | $\frac{3}{2}$ | B. | 9 | C. | $\sqrt{3}$ | D. | 64 |
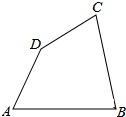 如图,凸四边形ABCD,求作一个三角形,使得该三角形的面积和凸四边形ABCD的面积相等.
如图,凸四边形ABCD,求作一个三角形,使得该三角形的面积和凸四边形ABCD的面积相等.