题目内容
17.在直角坐标系中画出下列双曲线的草图,并求实轴和虚轴的长、焦距、离心率.(1)$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1;
(2)16x2-9y2=-144.
分析 求出双曲线的几何量,即可求实轴和虚轴的长、焦距、离心率.
解答 解:(1)$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1中a=4,b=3,c=5,∴实轴长为8和虚轴长为6、焦距为10、离心率$\frac{5}{4}$;
(2)16x2-9y2=-144可化为$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{16}$=1.a=3,b=4,c=5,∴实轴长为6和虚轴长为10、焦距为10、离心率$\frac{5}{3}$.
如图所示.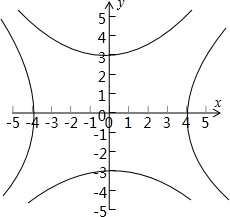
点评 本题考查双曲线的方程与性质,考查双曲线的图象,正确求出双曲线的几何量是关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
5.若锐角三角形的三边长分别为a-1,a,a+1,则a的取值范围是( )
| A. | (1,2) | B. | (2,3) | C. | (3,4) | D. | (4,+∞) |
12.已知等比数列{an}中,a1-a3+a5=2,a3-a5+a7=5,那么a5-a7+a9=( )
| A. | 8 | B. | 15 | C. | 25 | D. | $\frac{25}{2}$ |
2.设函数g(x)是定义在R上的可导函数,其导函数为g′(x),且3g(x)+xg′(x)>0恒成立,则不等式(x-2015)3g(x-2015)+8g(-2)>0的解集为( )
| A. | (-∞,-2013) | B. | (-2013,0) | C. | (2013,+∞) | D. | (0,2013) |