题目内容
已知函数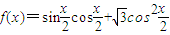 .
.(Ⅰ)当x∈[-
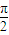 ,
,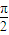 ]时,求函数f(x)的值域;
]时,求函数f(x)的值域;(Ⅱ)将函数f(x)的图象按向量
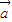 =(h,
=(h,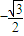 )(0<h<π)平移,使得平移后的函数g(x)的图象关于直线
)(0<h<π)平移,使得平移后的函数g(x)的图象关于直线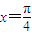 对称,求函数g(x)的单调递增区间.
对称,求函数g(x)的单调递增区间.
【答案】分析:(Ⅰ)利用辅助角公式把所给式子化成一个角的一个三角函数值,然后根据自变量x的取值范围,得x+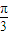 的范围,根据正弦函数的图象得sin(x+
的范围,根据正弦函数的图象得sin(x+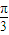 )的范围,最后得整个式子的范围,即函数f(x)的值域;
)的范围,最后得整个式子的范围,即函数f(x)的值域;
(Ⅱ)由向量的坐标可知,函数f(x)的图象向左平移h个单位,再向下平移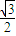 个单位,根据平移的规律得平移后的解析式,把x-h+
个单位,根据平移的规律得平移后的解析式,把x-h+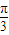 看为一个整体,令其等于正弦函数的对称轴,当x=
看为一个整体,令其等于正弦函数的对称轴,当x=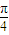 时,求出h的值,得具体解析式,把角代入正弦函数的增区间,得x的范围,即函数g(x)的单调递增区间.
时,求出h的值,得具体解析式,把角代入正弦函数的增区间,得x的范围,即函数g(x)的单调递增区间.
解答:解:(1)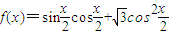 =
= =
=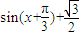
∵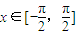 ,∴
,∴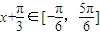 ,∴
,∴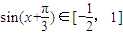
∴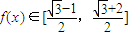
所以函数f(x)的值域是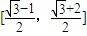
(2)平移后的函数为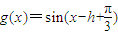 ,
,
令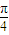 -h+
-h+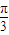 =
=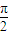 +kπ,得h=
+kπ,得h=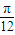 -kπ(k∈Z),
-kπ(k∈Z),
∵0<h<π,∴h=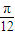
故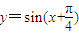 ,由
,由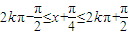
得
所以函数g(x)的单调增区间为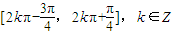
点评:求三角函数值域时,一般要把式子化为y=Asin(ωx+φ)的形式,从x的范围由里向外扩,利用数形结合,一直扩到Asin(ωx+φ)的范围,即函数f(x)的值域;求y=Asin(ωx+φ)的对称轴方程、单调递增区间时,要把ωx+φ看作整体,分别代入正弦函数的对称轴方程、单调递增区间,分别求出x得函数f(x)的对称轴方程、单调递增区间,这儿利用整体的思想.本题特色,结合了图象的平移.
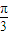 的范围,根据正弦函数的图象得sin(x+
的范围,根据正弦函数的图象得sin(x+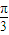 )的范围,最后得整个式子的范围,即函数f(x)的值域;
)的范围,最后得整个式子的范围,即函数f(x)的值域;(Ⅱ)由向量的坐标可知,函数f(x)的图象向左平移h个单位,再向下平移
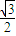 个单位,根据平移的规律得平移后的解析式,把x-h+
个单位,根据平移的规律得平移后的解析式,把x-h+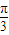 看为一个整体,令其等于正弦函数的对称轴,当x=
看为一个整体,令其等于正弦函数的对称轴,当x=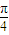 时,求出h的值,得具体解析式,把角代入正弦函数的增区间,得x的范围,即函数g(x)的单调递增区间.
时,求出h的值,得具体解析式,把角代入正弦函数的增区间,得x的范围,即函数g(x)的单调递增区间.解答:解:(1)
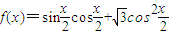 =
= =
=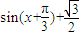
∵
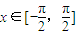 ,∴
,∴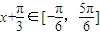 ,∴
,∴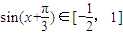
∴
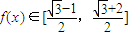
所以函数f(x)的值域是
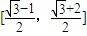
(2)平移后的函数为
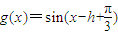 ,
,令
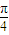 -h+
-h+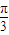 =
=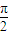 +kπ,得h=
+kπ,得h=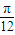 -kπ(k∈Z),
-kπ(k∈Z),∵0<h<π,∴h=
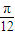
故
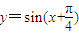 ,由
,由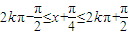
得

所以函数g(x)的单调增区间为
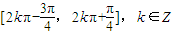
点评:求三角函数值域时,一般要把式子化为y=Asin(ωx+φ)的形式,从x的范围由里向外扩,利用数形结合,一直扩到Asin(ωx+φ)的范围,即函数f(x)的值域;求y=Asin(ωx+φ)的对称轴方程、单调递增区间时,要把ωx+φ看作整体,分别代入正弦函数的对称轴方程、单调递增区间,分别求出x得函数f(x)的对称轴方程、单调递增区间,这儿利用整体的思想.本题特色,结合了图象的平移.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目