题目内容
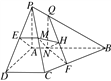
【题目】如图所示，四棱锥P－ABCD中，AB⊥AD，AD⊥DC，PA⊥底面ABCD， 
，M为PC的中点，N点在AB上且
.
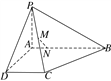
(1)证明：MN∥平面PAD；
(2)求直线MN与平面PCB所成的角．
【答案】（1）见解析；（2）
【解析】试题分析：（1）过点M作ME∥CD交PD于E点，则根据平几知识可得AEMN为平行四边形，即EM∥AN，再根据线面平行判定定理证结论（2）过N点作NQ∥AP交BP于点Q， NF⊥CB于点F，则易得面NQF垂直平面PCB，再过N点作NH⊥QF于点H，由面面垂直性质定理得NH⊥平面PBC，因此可得∠NMH为直线MN与平面PCB所成角，最后解三角形得直线MN与平面PCB所成的角．
试题解析：证明 (1)过点M作ME∥CD交PD于E点，连接AE，
∵AN＝
NB，∴AN＝
AB＝
DC＝EM，
又EM∥DC∥AB，∴EM∥AN，
∴四边形AEMN为平行四边形，∴MN∥AE，
又∵AE平面PAD，MN平面PAD，∴MN∥平面PAD.
(2)过N点作NQ∥AP交BP于点Q，
NF⊥CB于点F，连接QF，过N点作NH⊥QF于点H，
连接MH，易知QN⊥平面ABCD，
∴QN⊥BC，又NF⊥BC，NF∩QN＝N，NF平面QNF，QN平面QNF，
∴BC⊥平面QNF，∴BC⊥NH，
∵NH⊥QF，BC∩QF＝F，BC平面PBC，QF平面PBC，∴NH⊥平面PBC，
∴∠NMH为直线MN与平面PCB所成角，
通过计算可得MN＝AE＝
，QN＝
，NF＝
，
∴NH＝
＝
＝
，
∴sin∠NMH＝
＝
，∴∠NMH＝60°，∴直线MN与平面PCB所成角为60°.
练习册系列答案
通城学典默写能手系列答案
相关题目
