Question

【题目】已知函数，则关于的方程（）的实根个数（ ）

A.B. 或C.或 D.或

Answer 1

【答案】A

【解析】

先利用导数研究函数的单调性和极值，画出函数的大致图象，令，则，由△＞0可知方程有两个不相等的实根．设为,

由韦达定理得：,，不妨设，，对,的大小分情况讨论，结合函数的图象即可判断关于的方程（）的实根个数．

解：∵函数

∴，

令得：或，

∴当时，，函数单调递增；当时，，函数单调递减；当时，，函数单调递增，

又，，

∴函数的大致图象，如图所示：

，

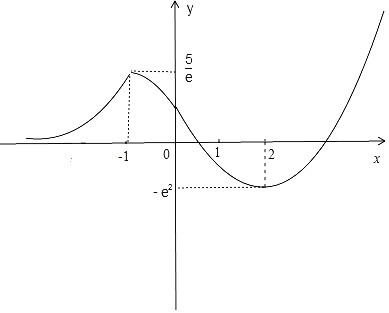令，则关于的方程变为，

∵，∴方程有两个不相等的实根．设为,

由韦达定理得：,，不妨设，，

①当时，∵，∴，此时关于的方程的实根个数为3个，

②当，∵，∴，此时关于的方程的实根个数为3个，

③当，∵，∴，此时关于的方程的实根个数为3个，

综上所述，关于的方程的实根个数为3个，

故选：A．