题目内容
在平面直角坐标系xOy中,已知椭圆C的中心在原点O,焦点在x轴上,短轴长为2,离心率为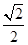 .
.
(1)求椭圆C的方程;
(2)A,B为椭圆C上满足△AOB的面积为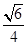 的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设
的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设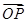 =t
=t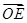 ,求实数t的值.
,求实数t的值.
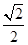 .
.(1)求椭圆C的方程;
(2)A,B为椭圆C上满足△AOB的面积为
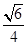 的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设
的任意两点,E为线段AB的中点,射线OE交椭圆C于点P.设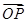 =t
=t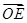 ,求实数t的值.
,求实数t的值.(1)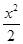 +y2=1(2)t=2或t=
+y2=1(2)t=2或t=
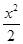 +y2=1(2)t=2或t=
+y2=1(2)t=2或t=
(1)设椭圆C的方程为 =1(a>b>0),
=1(a>b>0),
由题意知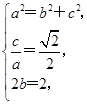 解得
解得
因此椭圆C的方程为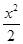 +y2=1.
+y2=1.
(2)(ⅰ)当A,B两点关于x轴对称时,设直线AB的方程为x=m.
由题意得- <m<0或0<m<
<m<0或0<m< .
.
将x=m代入椭圆方程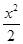 +y2=1,得|y|=
+y2=1,得|y|= .
.
所以S△AOB=|m|· =
=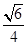 .解得m2=
.解得m2= 或m2=
或m2= .①
.①
因为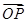 =t
=t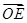 =
= t(
t( +
+ )=
)= t(2m,0)=(mt,0),
t(2m,0)=(mt,0),
又P为椭圆C上一点,所以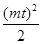 =1.②
=1.②
由①②,得t2=4或t2= ,
,
又t>0,所以t=2或t= .
.
(ⅱ)当A,B两点关于x轴不对称时,设直线AB的方程为y=kx+h.
将其代入椭圆的方程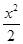 +y2=1,得
+y2=1,得
(1+2k2)x2+4khx+2h2-2=0.设A(x1,y1),B(x2,y2).
由判别式Δ>0可得1+2k2>h2,
此时x1+x2=-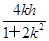 ,x1x2=
,x1x2= ,
,
y1+y2=k(x1+x2)+2h= ,
,
所以|AB|= .
.
因为点O到直线AB的距离d= ,
,
所以S△AOB= |AB|d=
|AB|d= ×2
×2 ×
× ×
× ×
× =
= ×
×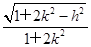 ×|h|.
×|h|.
又S△AOB=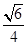 ,所以
,所以 ×
×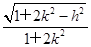 ×|h|=
×|h|=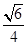 .③
.③
令n=1+2k2,代入③整理得3n2-16h2n+16h4=0.
解得n=4h2或n= h2,即1+2k2=4h2或1+2k2=
h2,即1+2k2=4h2或1+2k2= h2.④
h2.④
因为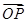 =t
=t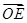 =
= t(
t( +
+ )=
)= t(x1+x2,y1+y2)=
t(x1+x2,y1+y2)=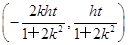 ,
,
又P为椭圆C上一点,
所以t2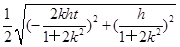 =1,即
=1,即 =1.⑤
=1.⑤
将④代入⑤,得t2=4或t2= .
.
又t>0,故t=2或t= .
.
经检验,适合题意.
综合(ⅰ)(ⅱ),得t=2或t=
 =1(a>b>0),
=1(a>b>0),由题意知
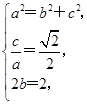 解得
解得
因此椭圆C的方程为
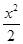 +y2=1.
+y2=1.(2)(ⅰ)当A,B两点关于x轴对称时,设直线AB的方程为x=m.
由题意得-
 <m<0或0<m<
<m<0或0<m< .
.将x=m代入椭圆方程
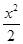 +y2=1,得|y|=
+y2=1,得|y|= .
.所以S△AOB=|m|·
 =
=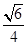 .解得m2=
.解得m2= 或m2=
或m2= .①
.①因为
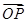 =t
=t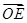 =
= t(
t( +
+ )=
)= t(2m,0)=(mt,0),
t(2m,0)=(mt,0),又P为椭圆C上一点,所以
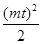 =1.②
=1.②由①②,得t2=4或t2=
 ,
,又t>0,所以t=2或t=
 .
.(ⅱ)当A,B两点关于x轴不对称时,设直线AB的方程为y=kx+h.
将其代入椭圆的方程
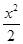 +y2=1,得
+y2=1,得(1+2k2)x2+4khx+2h2-2=0.设A(x1,y1),B(x2,y2).
由判别式Δ>0可得1+2k2>h2,
此时x1+x2=-
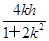 ,x1x2=
,x1x2= ,
,y1+y2=k(x1+x2)+2h=
 ,
,所以|AB|=
 .
.因为点O到直线AB的距离d=
 ,
,所以S△AOB=
 |AB|d=
|AB|d= ×2
×2 ×
× ×
× ×
× =
= ×
×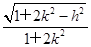 ×|h|.
×|h|.又S△AOB=
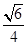 ,所以
,所以 ×
×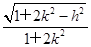 ×|h|=
×|h|=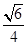 .③
.③令n=1+2k2,代入③整理得3n2-16h2n+16h4=0.
解得n=4h2或n=
 h2,即1+2k2=4h2或1+2k2=
h2,即1+2k2=4h2或1+2k2= h2.④
h2.④因为
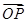 =t
=t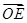 =
= t(
t( +
+ )=
)= t(x1+x2,y1+y2)=
t(x1+x2,y1+y2)=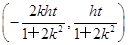 ,
,又P为椭圆C上一点,
所以t2
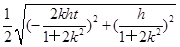 =1,即
=1,即 =1.⑤
=1.⑤将④代入⑤,得t2=4或t2=
 .
.又t>0,故t=2或t=
 .
.经检验,适合题意.
综合(ⅰ)(ⅱ),得t=2或t=


练习册系列答案
相关题目
 +
+ =1(a>b>0).
=1(a>b>0). ,求椭圆的标准方程.
,求椭圆的标准方程.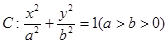 过点
过点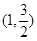 ,且离心率
,且离心率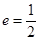 .
.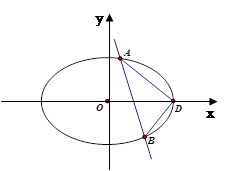
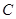 的标准方程;
的标准方程;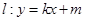 与椭圆
与椭圆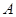 ,
,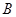 两点(
两点(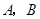 不是左右顶点),椭圆的右顶点为
不是左右顶点),椭圆的右顶点为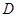 ,且满足
,且满足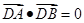 ,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.
,试判断直线是否过定点,若过定点,求出该定点的坐标;若不过定点,请说明理由.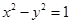 的焦点与椭圆
的焦点与椭圆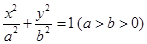 的焦点重合,且该椭圆的长轴长为
的焦点重合,且该椭圆的长轴长为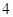 ,
,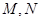 是椭圆上的的动点.
是椭圆上的的动点.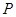 满足:
满足: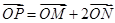 ,直线
,直线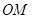 与
与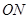 的斜率之积为
的斜率之积为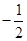 ,求证:存在定点
,求证:存在定点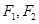 ,
,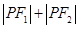 为定值,并求出
为定值,并求出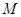 在第一象限,且点
在第一象限,且点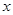 轴的射影为
轴的射影为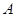 ,连接
,连接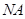 并延长交椭圆于
并延长交椭圆于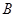 ,求证:以
,求证:以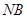 为直径的圆经过点
为直径的圆经过点 +
+ =1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )
=1(a>b>0)的右顶点和上顶点,直线l∥AB,l与x轴、y轴分别交于C,D两点,直线CE,DF为椭圆的切线,则CE与DF的斜率之积kCE·kDF等于( )

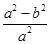


 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,a2与b2的等差中项为
,a2与b2的等差中项为 .
. =1,过点M(2,0)且斜率不为0的直线交椭圆C于A,B两点.在x轴上若存在定点P,使PM平分∠APB,则P的坐标为________.
=1,过点M(2,0)且斜率不为0的直线交椭圆C于A,B两点.在x轴上若存在定点P,使PM平分∠APB,则P的坐标为________.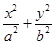 =1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为________.
=1(a>b>0)的右焦点为F(3,0),过点F的直线交椭圆于A,B两点.若AB的中点坐标为(1,-1),则E的方程为________.