题目内容
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,极轴为
,以极点为原点,极轴为![]() 轴正方向建立平面直角坐标系,曲线
轴正方向建立平面直角坐标系,曲线![]() 的直角坐标方程是
的直角坐标方程是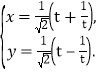 (
(![]() 为参数).
为参数).
(Ⅰ)将曲线![]() 的参数方程化为普通方程;
的参数方程化为普通方程;
(Ⅱ)求曲线![]() 与曲线
与曲线![]() 交点的极坐标.
交点的极坐标.
【答案】(1)![]() (2)
(2)![]() 与
与![]()
【解析】【试题分析】(I)利用加减消元法消去参数![]() ,可求得曲线
,可求得曲线![]() 的普通方程.(II)由(I)求得曲线
的普通方程.(II)由(I)求得曲线![]() 的极坐标方程,联立
的极坐标方程,联立![]() 的极坐标方程,可求得交点的极坐标.
的极坐标方程,可求得交点的极坐标.
【试题解析】
(Ⅰ)由曲线![]() 的参数方程得
的参数方程得![]() ,
,![]()
两式对应相乘得曲线![]() 的普通方程为
的普通方程为![]()
(Ⅱ)(方法一)将![]() ,
,![]() 代入上述方程得
代入上述方程得![]()
由![]() 得
得![]() ,代入得
,代入得![]() ,
,
解得![]() ,
,![]() 。
。
所以![]() ,
,![]() 或
或![]() ,所求交点的极坐标为
,所求交点的极坐标为![]() 与
与![]() 。
。
(方法二)由![]() 得
得![]() ,曲线
,曲线![]() 的直角坐标为
的直角坐标为![]()
解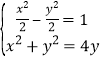 得
得![]() 或
或![]()
由![]() 得
得![]() ,
,![]() ,
,![]() ,
,![]() ,对应点的极坐标为
,对应点的极坐标为![]() ;
;
同理可得![]() 对应点的极坐标为
对应点的极坐标为![]() ,所求交点的极坐标为
,所求交点的极坐标为![]() 与
与![]() 。
。

【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() ,直线
,直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
【题目】中国政府实施“互联网+”战略以来,手机作为客户端越来越为人们所青睐,通过手机实现衣食住行消费已经成为一种主要的消费方式,“一机在手,走遍天下”的时代已经到来。在某著名的夜市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知其中从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有
列联表,并根据此资料判断是否有![]() 的把握认为“市场购物用手机支付与年龄有关”?
的把握认为“市场购物用手机支付与年龄有关”?
(2)现采用分层抽样从这100名顾客中按照“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本,设事件![]() 为“从这个样本中任选2人,这2人中至少有1人是不使用手机支付的”,求事件
为“从这个样本中任选2人,这2人中至少有1人是不使用手机支付的”,求事件![]() 发生的概率?
发生的概率?
|
|
|
|
|
|
|
|
|
|
![]() 列联表
列联表
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 24 | ||
合计 | 100 |
附:![]()
【题目】为了解某地区某种农产品的年产量x(单位:吨)对价格y(单位:千元/吨)和利润z的影响,对近五年该农产品的年产量和价格统计如下表:
x | 1 | 2 | 3 | 4 | 5 |
y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
(1)求y关于x的线性回归方程![]() ;
;
(2)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润z取到最大值?(保留两位小数)
参考公式: 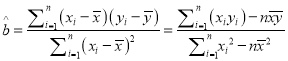 ,
, ![]()