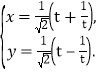题目内容
【题目】设函数![]() 有两个极值点
有两个极值点![]() ,
,![]() ,且
,且![]() .
.
(![]() )求
)求![]() 的取值范围,并讨论
的取值范围,并讨论![]() 的单调性.
的单调性.
(![]() )证明:
)证明:![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】试题分析 : (1)先确定函数的定义域然后求导数![]() ,由题意知
,由题意知![]() ,
,![]() 是方程
是方程![]() 的两个均大于-1的不相等的实根,建立不等关系解之即可,在函数的定义域内解不等式
的两个均大于-1的不相等的实根,建立不等关系解之即可,在函数的定义域内解不等式![]() 和
和![]() ,求出单调区间;
,求出单调区间;
(2)![]() 是方程
是方程![]() 的根,将
的根,将![]() 用
用![]() 表示,消去
表示,消去![]() 得到关于
得到关于![]() 的函数,研究函数的单调性求出函数的最大值,即可证得不等式.
的函数,研究函数的单调性求出函数的最大值,即可证得不等式.
试题解析 :
(![]() )由题意知,函数
)由题意知,函数![]() 的定义域是
的定义域是![]() ,
,
![]() ,
,
且![]() 有两个不同的实数根
有两个不同的实数根![]() ,
,![]() ,故
,故![]() 的判别式
的判别式![]() ,即
,即![]() ,且
,且![]() ,
,![]() ,①
,①
又![]() ,故
,故![]() .因此
.因此![]() 的取值范围是
的取值范围是![]() .
.
当![]() 变化时
变化时![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大值 |
| 极小值 |
|
因此![]() 在区间
在区间![]() 和
和![]() 是增函数,在
是增函数,在![]() 上是减函数.
上是减函数.
(![]() )由题意和①知,
)由题意和①知,![]() ,
,![]() ,
,
于是![]() .
.
设函数![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,故
,故![]() 在
在![]() 上是增函数.
上是增函数.
于是,当![]() ,
,![]() .因此
.因此![]() .
.

练习册系列答案
相关题目
【题目】某学校运动会的立定跳远和30秒跳绳两个单项比赛分成预赛和决赛两个阶段.下表为10名学生的预赛成绩,其中有三个数据模糊.
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
立定跳远(单位:米) | 1.96 | 1.92 | 1.82 | 1.80 | 1.78 | 1.76 | 1.74 | 1.72 | 1.68 | 1.60 |
30秒跳绳(单位:次) | 63 | a | 75 | 60 | 63 | 72 | 70 | a1 | b | 65 |
在这10名学生中,进入立定跳远决赛的有8人,同时进入立定跳远决赛和30秒跳绳决赛的有6人,则
(A)2号学生进入30秒跳绳决赛
(B)5号学生进入30秒跳绳决赛
(C)8号学生进入30秒跳绳决赛
(D)9号学生进入30秒跳绳决赛