题目内容
已知偶函数y=f(x)对任意实数x都有f(x+1)=-f(x),且在[0,1]上单调递减,则
- A.
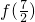 <
<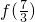 <
<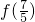
- B.
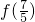 <
<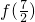 <
<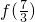
- C.
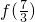 <
<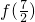 <
<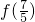
- D.
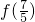 <
<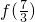 <
<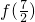
B
分析:先根据f(x+1)=-f(x)判断函数为以2的周期函数,再通过周期性把f( ),f(
),f( ),f(
),f( )分别转化成f(
)分别转化成f( ),f(
),f( ),f(
),f( ),进而根据函数在[0,1]上单调递减进而得到答案.
),进而根据函数在[0,1]上单调递减进而得到答案.
解答:f(x+2)=f(x+1+1)=-f(x+1)=f(x),
∴f(x)是以2为周期的函数.
∴f( )=f(
)=f( -4)=f(-
-4)=f(- )=f(
)=f( ),f(
),f( )=f(2+
)=f(2+ )=f(
)=f( ),f(
),f( )=f(
)=f(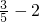 )=f(
)=f( )
)
在[0,1]上单调递减,∴f( )<f(
)<f( )<f(
)<f( )
)
∴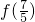 <
<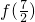 <
<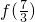
故选B
点评:本题主要考查了函数的奇偶性和单调性的综合运用.属基础题.
分析:先根据f(x+1)=-f(x)判断函数为以2的周期函数,再通过周期性把f(
 ),f(
),f( ),f(
),f( )分别转化成f(
)分别转化成f( ),f(
),f( ),f(
),f( ),进而根据函数在[0,1]上单调递减进而得到答案.
),进而根据函数在[0,1]上单调递减进而得到答案.解答:f(x+2)=f(x+1+1)=-f(x+1)=f(x),
∴f(x)是以2为周期的函数.
∴f(
 )=f(
)=f( -4)=f(-
-4)=f(- )=f(
)=f( ),f(
),f( )=f(2+
)=f(2+ )=f(
)=f( ),f(
),f( )=f(
)=f(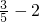 )=f(
)=f( )
)在[0,1]上单调递减,∴f(
 )<f(
)<f( )<f(
)<f( )
)∴
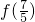 <
<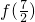 <
<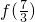
故选B
点评:本题主要考查了函数的奇偶性和单调性的综合运用.属基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
已知偶函数y=f(x)在[-1,0]上为单调递减函数,又α、β为锐角三角形的两内角,则( )
| A、f(sinα)>f(cosβ) | B、f(sinα)<f(cosβ) | C、f(sinα)>f(sinβ) | D、f(cosα)>f(cosβ) |