题目内容
(本小题共14分)
在平面直角坐标系xOy中,点B与点A(-1,1)关于原点O对称,P是动点,且直线AP与BP的斜率之积等于![]() .
.
(Ⅰ)求动点P的轨迹方程;
(Ⅱ)设直线AP和BP分别与直线x=3交于点M,N,问:是否存在点P使得△PAB与△PMN的面积相等?若存在,求出点P的坐标;若不存在,说明理由。
解:(1)因点B与(-1,1)关于原点对称,得B点坐标为(1,-1)。
设P点坐标为![]() ,则
,则![]() ,由题意得
,由题意得![]() ,
,
化简得:![]() 。
。
即P点轨迹为:![]()
(2)因![]() ,可得
,可得![]() ,
,
又![]() ,
,
若![]() ,则有
,则有![]() , 即
, 即![]()
设P点坐标为![]() ,则有:
,则有:![]()
解得:![]() ,又因
,又因![]() ,解得
,解得![]() 。
。
故存在点P使得![]() 与
与![]() 的面积相等,此时P点坐标为
的面积相等,此时P点坐标为![]() 或
或![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 底面ABCD,PD=DC,点E是PC的中点,作EF
底面ABCD,PD=DC,点E是PC的中点,作EF
 的棱长为
的棱长为 ,
, 是
是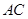 与
与 的交点,
的交点, 为
为 的中点.
的中点. ∥平面
∥平面 ;
; 平面
平面 ;
; 的体积.
的体积.