题目内容
(2009北京理)(本小题共14分)
已知双曲线![]() 的离心率为
的离心率为![]() ,右准线方程为
,右准线方程为![]()
(Ⅰ)求双曲线![]() 的方程;
的方程;
(Ⅱ)设直线![]() 是圆
是圆![]() 上动点
上动点![]() 处的切线,
处的切线,![]() 与双曲线
与双曲线![]() 交
交
于不同的两点![]() ,证明
,证明![]() 的大小为定值.
的大小为定值.
【解法1】本题主要考查双曲线的标准方程、圆的切线方程等基础知识,考查曲线和方程
的关系等解析几何的基本思想方法,考查推理、运算能力.
(Ⅰ)由题意,得 ,解得
,解得![]() ,
,
∴![]() ,∴所求双曲线
,∴所求双曲线![]() 的方程为
的方程为![]() .
.
(Ⅱ)点![]() 在圆
在圆![]() 上,
上,
圆在点![]() 处的切线方程为
处的切线方程为![]() ,
,
化简得![]() .
.
由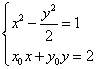 及
及![]() 得
得![]() ,
,
∵切线![]() 与双曲线C交于不同的两点A、B,且
与双曲线C交于不同的两点A、B,且![]() ,
,
∴![]() ,且
,且![]() ,
,
设A、B两点的坐标分别为![]() ,
,
则![]() ,
,
∵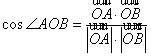 ,且
,且
![]() ,
,
![]()

![]() .
.
∴ ![]() 的大小为
的大小为![]() .
.
【解法2】(Ⅰ)同解法1.
(Ⅱ)点![]() 在圆
在圆![]() 上,
上,
圆在点![]() 处的切线方程为
处的切线方程为![]() ,
,
化简得![]() .由
.由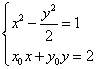 及
及![]() 得
得
![]() ①
①
![]() ②
②
∵切线![]() 与双曲线C交于不同的两点A、B,且
与双曲线C交于不同的两点A、B,且![]() ,
,
∴![]() ,设A、B两点的坐标分别为
,设A、B两点的坐标分别为![]() ,
,
则![]() ,
,
∴![]() ,∴
,∴ ![]() 的大小为
的大小为![]() .
.
(∵![]() 且
且![]() ,∴
,∴![]() ,从而当
,从而当![]() 时,方程①和方程②的判别式均大于零).
时,方程①和方程②的判别式均大于零).

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
