题目内容
关于方程3x+x2+2x-1=0,下列说法正确的是 ( )
| A.方程有两不相等的负实根 | B.方程有两个不相等的正实根 |
| C.方程有一正实根,一零根 | D.方程有一负实根,一零根 |
D
分析:构造函数y1=3x,y2=-x2-2x+1=-(x+1)2+2,图象分别为指数函数与对称轴为直线x=-1,顶点坐标为(-1,2)的抛物线,由此可得结论.
解答:解:构造函数y1=3x,y2=-x2-2x+1=-(x+1)2+2,图象分别为指数函数与对称轴为直线x=-1,顶点坐标为(-1,2)的抛物线,如图所示
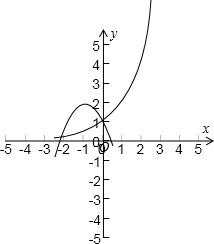
显然(0,1),是两个图象的一个交点,另一个交点的横坐标小于0
所以方程3x+x2+2x-1=0方程有一负实根,一零根
故选D.
点评:本题考查方程根的研究,解题的关键是构造函数,转化为图象的交点问题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
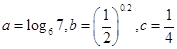 ,则
,则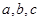 的大小关系是
的大小关系是 



 是
是 上的奇函数,当
上的奇函数,当 时,
时, ,
, 上的单调性;
上的单调性; 的解集。
的解集。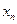 表示某鱼群在第
表示某鱼群在第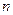 年初的总量,
年初的总量,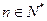 ,且
,且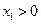 。不考虑其他因素,设在第
。不考虑其他因素,设在第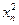 成正比,这些比例系数依次为正数
成正比,这些比例系数依次为正数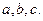 其中
其中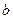 称为捕捞强度。
称为捕捞强度。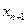 与
与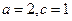 ,为了保证对任
,为了保证对任 意
意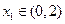 ,都有
,都有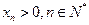 ,则捕捞强度
,则捕捞强度 ,其中
,其中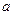 为大于零的常数.
为大于零的常数.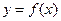 在点(1,
在点(1,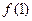 )处的切线与直线
)处的切线与直线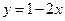 平行,求
平行,求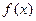 在区间[1,2]上的最小值.
在区间[1,2]上的最小值. 的零点为2,那么函数
的零点为2,那么函数 的零点是( )
的零点是( )

 ,
, ,若存在
,若存在 ,使得
,使得 成立,称
成立,称 为不动点,已知函数
为不动点,已知函数
 时,求函数
时,求函数 不动点.
不动点. ,函数
,函数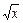 +
+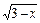 的最大值为 .
的最大值为 .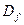 、
、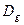 的函数
的函数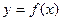 、
、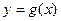 ,规定:函数
,规定:函数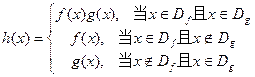 ,若函数
,若函数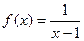 ,
,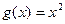 ,则
,则 。
。