题目内容
(本题满分12分)已知函数 是
是 上的奇函数,当
上的奇函数,当 时,
时, ,
,
(1)判断并证明 在
在 上的单调性;
上的单调性;
(2)求 的值域;
的值域;
(3)求不等式 的解集。
的解集。
 是
是 上的奇函数,当
上的奇函数,当 时,
时, ,
,(1)判断并证明
 在
在 上的单调性;
上的单调性;(2)求
 的值域;
的值域; (3)求不等式
 的解集。
的解集。解:(1)设 ,则
,则 ,
,
∵ ,
,
∴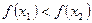 ,即
,即 在
在 上是增函数。
上是增函数。
(2)∵ ,∴当
,∴当 时,
时, ;
;
∵当 时,
时,
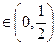 。
。
综上得 的值域为
的值域为 。
。
(3)∵ ,又∵
,又∵ ,∴
,∴ ,
,
此时 单调递增, ∵
单调递增, ∵ ,
,
∴ 时,
时, 。令
。令 ,
,
即 ,
,
∴不等式 的解集是
的解集是
 ,则
,则 ,
,
∵
 ,
,∴
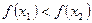 ,即
,即 在
在 上是增函数。
上是增函数。(2)∵
 ,∴当
,∴当 时,
时, ;
;∵当
 时,
时,
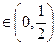 。
。综上得
 的值域为
的值域为 。
。(3)∵
 ,又∵
,又∵ ,∴
,∴ ,
,此时
 单调递增, ∵
单调递增, ∵ ,
,∴
 时,
时, 。令
。令 ,
,即
 ,
,∴不等式
 的解集是
的解集是
略

练习册系列答案
相关题目
 若f(f (1))=1,则a=________.
若f(f (1))=1,则a=________. .
. 的不等式
的不等式 ;
;
 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围. 万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值
万元的激光器生产线,计划通过技术改造来提高该生产线的生产能力,提高产品的增加值. 经过市场调查,产品的增加值 万元与技术改造投入
万元与技术改造投入 万元之间满足:①
万元之间满足:① 成正比;②当
成正比;②当 时,
时, ,并且技术改造投入满足
,并且技术改造投入满足 ,其中
,其中 为常数且
为常数且 .
. 表达式及定义域;
表达式及定义域; 上的函数
上的函数 ,满足
,满足 ,求证:函数
,求证:函数 在
在 上的可导函数,满足
上的可导函数,满足 ,则
,则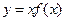 是
是 :
: ,若
,若  +
+
 ,
, 若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是_______
若关于x 的方程f(x)=k有两个不同的实根,则数k的取值范围是_______ 的定义域为_________
的定义域为_________ 的最大值为
的最大值为