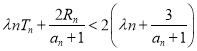题目内容
【题目】袋中装有10个除颜色外完全一样的黑球和白球，已知从袋中任意摸出2个球，至少得到1个白球的概率是
.
（1）求白球的个数；
（2）从袋中任意摸出3个球，记得到白球的个数为X,求随机变量X的分布列.
【答案】（1）5个；（2）见解析.
【解析】
（1）设白球的个数为x，则黑球的个数为10﹣x，记“从袋中任意摸出2个球，至少得到1个白球”为事件A，则两个都是黑球与事件A为对立事件，由此能求出白球的个数；（2）随机变量X的取值可能为：0，1，2，3，分别求出相应的概率，由此能求出X的分布列．
（1）设白球的个数为x，则黑球的个数为10﹣x，记“从袋中任意摸出2个球，至少得到1个白球”为事件A，则
,解得
.故白球有5个.
（2）X服从以10，5，3为参数的超几何分布，
.
于是可得其分布列为:
|
|
|
|
|
|
|
|
|
|
【题目】某工厂生产
，
，
三种纪念品，每种纪念品均有普通型和精品型两种，某一天产量如下表（单位：个）：
普通型 | 精品型 | |
纪念品 | 800 | 200 |
纪念品 |
| 150 |
纪念品 | 500 | 350 |
现采用分层抽样的方法在这一天生产的纪念品中抽取100个，其中有种纪念品40个.
（1）若再用分层抽样的方法在所有种纪念品中抽取一个容量为13的样本.将该样本看成一个总体，从中任取2个纪念品，求至少有1个精品型纪念品的概率（用最简分数表示）；
（2）从种精品型纪念品中抽取6个，其某种指标的数据分别如下：4，7，
，
，8，5.把这6个数据看作一个总体，其均值为7、方差为6，求
的值.
【题目】为了解某冷饮店的经营状况，随机记录了该店
月的月营业额
（单位：万元）与月份
的数据，如下表：
|
|
|
|
|
|
|
|
|
|
|
|
（1）求关于的回归直线方程
；
（2）若在这样本点中任取两点，求恰有一点在回归直线上的概率.
附：回归直线方程中，
，
.
【题目】某校学生会为研究该校学生的性别与语文、数学、英语成绩这3个变量之间的关系，随机抽查了100名学生，得到某次期末考试的成绩数据如表1至表3，根据表中数据可知该校学生语文、数学、英语这三门学科中（ ）
表1 | 表2 | 表3 | |||||||||||||
语文 性别 | 不及格 | 及格 | 总计 | 数学 性别 | 不及格 | 及格 | 总计 | 英语 性别 | 不及格 | 及格 | 总计 | ||||
男 | 14 | 36 | 50 | 男 | 10 | 40 | 50 | 男 | 25 | 25 | 50 | ||||
女 | 16 | 34 | 50 | 女 | 20 | 30 | 50 | 女 | 5 | 45 | 50 | ||||
总计 | 30 | 70 | 100 | 总计 | 30 | 70 | 100 | 总计 | 30 | 70 | 100 | ||||
A.语文成绩与性别有关联性的可能性最大，数学成绩与性别有关联性的可能性最小
B.数学成绩与性别有关联性的可能性最大，语文成绩与性别有关联性的可能性最小
C.英语成绩与性别有关联性的可能性最大，语文成绩与性别有关联性的可能性最小
D.英语成绩与性别有关联性的可能性最大，数学成绩与性别有关联性的可能性最小