题目内容
(理科)设函数f(x)的定义域为R,若存在常数 M>0,使|f(x)|≤M|x|对一切实数 x均成立,则f(x)为β函数.现给出如下4个函数:(1)f(x)=0;f(x)=x2;f(x)=
(sinx+cosx);f(x)=
.其中是β函数的序号是
| 2 |
| x |
| x2+x+1 |
(1)(4)
(1)(4)
.分析:对于(1)取M>0的任意一值都符合定义,对于(2)不存在这样的M满足定义,对于(3)由于x=0时,|f(x)|≤M|x|不成立,不满足定义,对于(4),|f(x)|=
|x|≤
|x|,故对任意的M≥
满足定义,可得结论.
| 1 |
| x2+x+1 |
| 4 |
| 3 |
| 4 |
| 3 |
解答:解:由题意
对于(1)f(x)=0,显然对任意常数M>0,均成立,故f(x)为β函数;
对于(2),|f(x)|≤M|x|,显然不成立,故其不是β函数;
对于(3),f(x)=
(sinx+cosx),由于x=0时,|f(x)|≤M|x|不成立,故不是β函数;
对于(4),f(x)=
,|f(x)|=
|x|≤
|x|,故对任意的M≥
,都有|f(x)|≤M|x|,故是β函数;
故答案为:(1)(4)
对于(1)f(x)=0,显然对任意常数M>0,均成立,故f(x)为β函数;
对于(2),|f(x)|≤M|x|,显然不成立,故其不是β函数;
对于(3),f(x)=
| 2 |
对于(4),f(x)=
| x |
| x2+x+1 |
| 1 |
| x2+x+1 |
| 4 |
| 3 |
| 4 |
| 3 |
故答案为:(1)(4)
点评:本题主要考查了函数恒成立问题,主要考查根据所给的新定义来验证函数是否满足定义中的规则,属于中档题.

练习册系列答案
相关题目
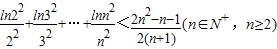 .
.