题目内容
(理科)设函数f(x)=lnx-x+1,(Ⅰ)求f(x)的单调区间;
(Ⅱ)求证:lnx≤x-1;
(Ⅲ)证明:
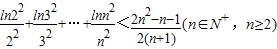 .
.
【答案】分析:(Ⅰ)由导数f'(x)>0求得x的范围,即为函数的增区间,同理,由导数f'(x)<0求得x的范围,即为函数的减区间.
(Ⅱ)由(Ⅰ)知:当x=1时,f(x)max=-1+1=0.故对任意x>0,有f(x)≤0,由此化简可得要证的不等式.
(Ⅲ)由(Ⅱ)知,当x≥2时,则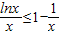 ,
,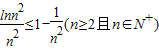 ,故不等式的左边小于
,故不等式的左边小于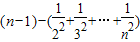 ,再由
,再由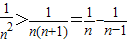 ,可得
,可得
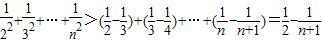 ,从而证得不等式成立.
,从而证得不等式成立.
解答:解:(Ⅰ)由已知得 ,由f'(x)>0,得
,由f'(x)>0,得 ,
,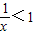 ,x>1.
,x>1.
∴f(x)在(1,+∞)上为减函数,在(0,1)为增函数.…(4分)
(Ⅱ)由(Ⅰ)知:当x=1时,f(x)max=-1+1=0.
对任意x>0,有f(x)≤0,即lnx-x+1≤0. 即lnx≤x-1.…(8分)
(Ⅲ)由(Ⅱ)知,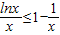 ,当x≥2时,则
,当x≥2时,则 ,
,
∴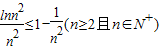 ,∴
,∴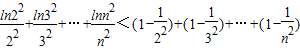 =
=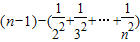
又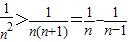 ,
,
∴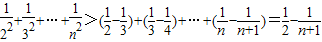
故不等式的左边小于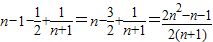 ,故要证的不等式成立.…(14分)
,故要证的不等式成立.…(14分)
点评:本题主要考查利用导数研究函数的单调性,用放缩法证明不等式,体现了转化的数学思想,其中,用放缩法证明不等式,是解题的难点.
(Ⅱ)由(Ⅰ)知:当x=1时,f(x)max=-1+1=0.故对任意x>0,有f(x)≤0,由此化简可得要证的不等式.
(Ⅲ)由(Ⅱ)知,当x≥2时,则
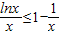 ,
,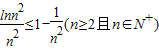 ,故不等式的左边小于
,故不等式的左边小于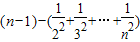 ,再由
,再由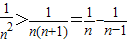 ,可得
,可得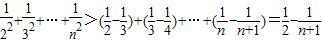 ,从而证得不等式成立.
,从而证得不等式成立.解答:解:(Ⅰ)由已知得
 ,由f'(x)>0,得
,由f'(x)>0,得 ,
,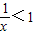 ,x>1.
,x>1.∴f(x)在(1,+∞)上为减函数,在(0,1)为增函数.…(4分)
(Ⅱ)由(Ⅰ)知:当x=1时,f(x)max=-1+1=0.
对任意x>0,有f(x)≤0,即lnx-x+1≤0. 即lnx≤x-1.…(8分)
(Ⅲ)由(Ⅱ)知,
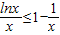 ,当x≥2时,则
,当x≥2时,则 ,
,∴
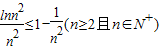 ,∴
,∴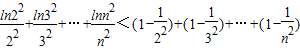 =
=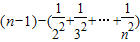
又
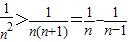 ,
,∴
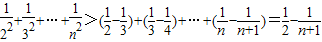
故不等式的左边小于
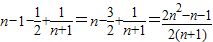 ,故要证的不等式成立.…(14分)
,故要证的不等式成立.…(14分)点评:本题主要考查利用导数研究函数的单调性,用放缩法证明不等式,体现了转化的数学思想,其中,用放缩法证明不等式,是解题的难点.

练习册系列答案
相关题目