题目内容
(理科)设函数f(x)的定义域为{x|x≠0},值域为R且同时满足下列条件:
(1)对于任意非零实数x1,x2,都有f(x1x2)=f(x1)+f(x2);
(2)对于任意正数x1,x2,且x1≠x2,都有
>0.
出符合上述条件的一个函数f(x)
(1)对于任意非零实数x1,x2,都有f(x1x2)=f(x1)+f(x2);
(2)对于任意正数x1,x2,且x1≠x2,都有
| f(x1)-f(x2) | x1-x2 |
出符合上述条件的一个函数f(x)
=log2|x|(答案不唯一)
=log2|x|(答案不唯一)
.分析:根据题意,联系常见的函数,分析条件(1),有数函数符合f(x1x2)=f(x1)+f(x2),分析(2)可得,f(x)为增函数,综合(1)、(2)可得f(x)的底数大于1的对数函数,据此即可写出答案.
解答:解:根据题意,
对于(1),要求函数的满足f(x1x2)=f(x1)+f(x2)的运算律,分析可得对数函数符合,
对于(2),若
>0,则f(x)在正实数集上为增函数,
对于对数函数,当底数大于1时,为增函数,
则符合条件(1)(2)的为底数大于1的对数函数,如y=log2|x|,y=log3|x|,y=lg|x|,等
故答案为log2|x|,(答案不唯一,只要为底数大于1的对数函数即可)
对于(1),要求函数的满足f(x1x2)=f(x1)+f(x2)的运算律,分析可得对数函数符合,
对于(2),若
| f(x1)-f(x2) |
| x1-x2 |
对于对数函数,当底数大于1时,为增函数,
则符合条件(1)(2)的为底数大于1的对数函数,如y=log2|x|,y=log3|x|,y=lg|x|,等
故答案为log2|x|,(答案不唯一,只要为底数大于1的对数函数即可)
点评:本题考查对数函数的性质,是开放性题目,关键是由f(x1x2)=f(x1)+f(x2)分析出该函数与对数函数有关.

练习册系列答案
相关题目
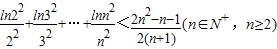 .
.