题目内容
(本题满分12分)
如图,四棱锥P—ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点。

(1)求证:CD⊥AE;
(2)求证:PD⊥面ABE。
如图,四棱锥P—ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点。

(1)求证:CD⊥AE;
(2)求证:PD⊥面ABE。
(1)要证明线线垂直,则只要根据线面垂直的性质定理可以证明。
(2)对于线面垂直的证明,一般先证明线线垂直,然后结合线面垂直的判定定理得到,关键是证明AE⊥PD和BA⊥PD。
(2)对于线面垂直的证明,一般先证明线线垂直,然后结合线面垂直的判定定理得到,关键是证明AE⊥PD和BA⊥PD。
试题分析:(I)证明:∵PA⊥底面ABCD
∴CD⊥PA
又CD⊥AC,PA∩AC=A,
故CD⊥面PAC
AE
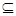 面PAC,故CD⊥AE
面PAC,故CD⊥AE (II)证明:PA=AB=BC,∠ABC=60°,
故PA=ACE是PC的中点,故AE⊥PC
由(I)知CD⊥AE,从而AE⊥面PCD,
故AE⊥PD
易知BA⊥PD,故PD⊥面ABE
点评:本试题考查了空间中线线与线面的位置关系的运用,关键是熟练的结合线线与线面垂直的判定定理和性质定理来得到证明,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
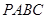 的六条边均相等,
的六条边均相等, 分别是
分别是 的中点,则下列四个结论中不成立的是 ( )
的中点,则下列四个结论中不成立的是 ( ) 
 平面
平面
 平面
平面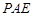
 //平面
//平面
 平面
平面 中,
中, 平面
平面 ,底面
,底面 是菱形,
是菱形, ,
, .
.

 ;
; ,求二面角
,求二面角 的余弦值.
的余弦值. ,
, ,
,
 ( )
( )



 是直线,
是直线, 是平面,给出下列命题:
是平面,给出下列命题: ,
, ,
, ,则
,则 或
或 .
. ,
, ,
, ,则
,则 .
.
 ,n
,n ,n∥
,n∥ 且
且 ,
, ,则
,则
 、
、 为两条不同的直线,
为两条不同的直线, 、
、 为两个不同的平面,则下列推理中正确的是( )
为两个不同的平面,则下列推理中正确的是( )




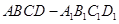 中,
中, ,点
,点 为
为 的中点,点
的中点,点 在
在 上,若
上,若 平面
平面 ,则
,则 ________.
________.