题目内容
设数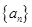 满足:
满足: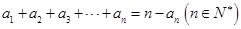 .
.
(1)求证:数列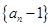 是等比数列;
是等比数列;
(2)若 ,且对任意的正整数
,且对任意的正整数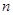 ,都有
,都有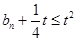 ,求实数
,求实数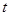 的取值范围.
的取值范围.
(1)详见解析;(2)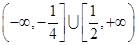 .
.
解析试题分析:(1)先令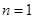 求出
求出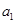 的值,然后令
的值,然后令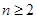 ,由
,由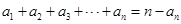 得到
得到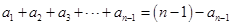 ,将两式相减得到
,将两式相减得到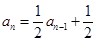 ,利用定义法证明数列
,利用定义法证明数列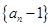 是
是
等比数列;(2)在(1)的基础上求出数列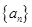 的通项公式,进而确定数列
的通项公式,进而确定数列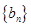 的通项公式,将不等式
的通项公式,将不等式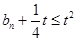 转化为
转化为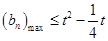 ,利用作差法研究数列
,利用作差法研究数列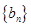 的单调性,确定数列
的单调性,确定数列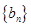 的最大项的值,
的最大项的值,
从而解出相应的不等式即可.
(1)当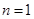 时,则有
时,则有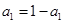 ,解得
,解得 ,
,
当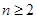 且
且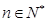 时,
时,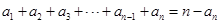 ,
,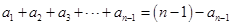 ,
,
上式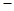 下式,得
下式,得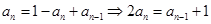 ,所以
,所以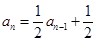 ,
,
故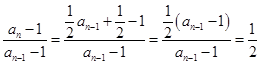 ,且
,且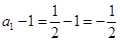
因此数列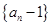 是首项为
是首项为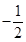 ,公比为
,公比为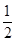 的等比数列,
的等比数列,
因此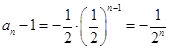 ;
;
(2)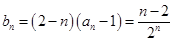 ,
,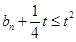 对任意的正整数
对任意的正整数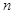 恒成立,则
恒成立,则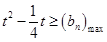 ,
,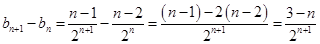 ,
,
当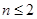 且
且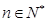 时,
时,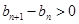 ,即
,即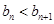 ,因此
,因此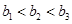 ,
,
当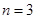 时,则
时,则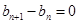 ,则有
,则有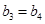 ,
,
当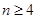 且
且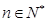 时,
时,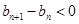 ,即
,即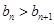 ,则数列从第四项开始单调递减,
,则数列从第四项开始单调递减,
因此,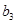 或
或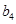 最大,
最大,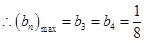 ,
,
所以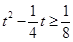 ,即
,即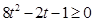 ,解得
,解得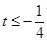 或
或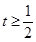 ,
,
因此实数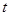 的取值范围是
的取值范围是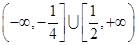 .
.
考点:1.定义法求数列通项;2.等比数列的定义;3.数列的单调性;4.不等式恒成立

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
已知等差数列 的前n项和为
的前n项和为 ,
,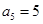 ,
,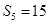 ,则数列
,则数列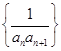 的前100项和为( )
的前100项和为( )
A. | B.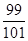 | C. | D.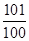 |
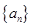 的通项为
的通项为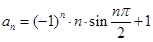 前
前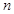 项和为
项和为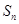 , 则
, 则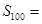 _________.
_________.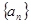 中, 已知
中, 已知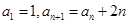 , 则
, 则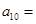 ________________;
________________;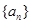 的前
的前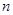 项和为
项和为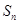 ,且
,且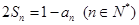 .
.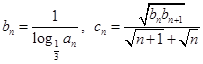 ,求数列
,求数列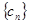 的前
的前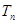 .
.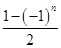 an-
an-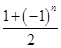 bn,求数列{cn}的前2n项和T2n.
bn,求数列{cn}的前2n项和T2n.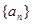 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第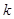 个1和第
个1和第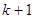 个1之间有
个1之间有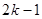 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前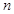 项的和为
项的和为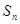 .参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
.参考:31×32=992,32×33=1056,44×45=1980,45×46=2070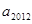 和
和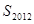 ;
;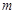 ,使得
,使得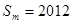 ?如果存在,求出
?如果存在,求出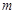 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.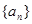 的前
的前 项和
项和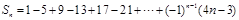 ,则
,则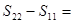 .
.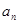 }中,
}中,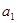 =
=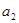 =1,
=1, 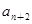 =
=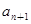 +
+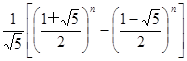 ,根据上述结论,可以知道不超过实数
,根据上述结论,可以知道不超过实数  的最大整数为
的最大整数为