题目内容
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA= ,则正三棱锥S-ABC的外接球的表面积为( )
,则正三棱锥S-ABC的外接球的表面积为( )
A.9π
B.12π
C.16π
D.32π
【答案】分析:由题意推出MN⊥平面SAC,即SB⊥平面SAC,∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球,正方体的对角线就是球的直径,求出直径即可求出球的表面积.
解答:解:∵三棱锥S-ABC正棱锥,∴SB⊥AC(对棱互相垂直)∴MN⊥AC
又∵MN⊥AM而AM∩AC=A,∴MN⊥平面SAC即SB⊥平面SAC
∴∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球
∴2R= ,∴R=
,∴R= ,∴S=4πR2=
,∴S=4πR2= ,
,
故选A.
点评:本题是基础题,考查三棱锥的外接球的表面积,考查空间想象能力,三棱锥扩展为正方体,它的对角线长就是外接球的直径,是解决本题的关键.
解答:解:∵三棱锥S-ABC正棱锥,∴SB⊥AC(对棱互相垂直)∴MN⊥AC
又∵MN⊥AM而AM∩AC=A,∴MN⊥平面SAC即SB⊥平面SAC
∴∠ASB=∠BSC=∠ASC=90°,将此三棱锥补成正方体,则它们有相同的外接球
∴2R=
 ,∴R=
,∴R= ,∴S=4πR2=
,∴S=4πR2= ,
,故选A.
点评:本题是基础题,考查三棱锥的外接球的表面积,考查空间想象能力,三棱锥扩展为正方体,它的对角线长就是外接球的直径,是解决本题的关键.

练习册系列答案
相关题目
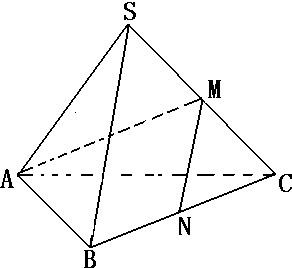 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
 ,则正三棱锥S-ABC的外接球的表面积为
,则正三棱锥S-ABC的外接球的表面积为
 B
B
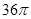
 D
D 
 ,则正三棱锥S-ABC的外接球的表面积为( )
,则正三棱锥S-ABC的外接球的表面积为( )