题目内容
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且MN⊥AM,若侧棱长SA= ,则正三棱锥S-ABC的外接球的表面积为
,则正三棱锥S-ABC的外接球的表面积为

A  B
B
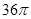
C 32 D
D 
【答案】
B
【解析】
试题分析:由条件中的MN⊥AM,可以推得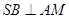 。
。
又由正三棱锥S-ABC中对棱互相垂直,得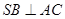 。所以SB⊥平面SAC,从而该正三棱锥的三个顶角都是直角。将该三棱锥补成正方体,使S成为正方体的一个顶点,则正三棱锥S-ABC的外接球也即是正方体的外接球,根据
。所以SB⊥平面SAC,从而该正三棱锥的三个顶角都是直角。将该三棱锥补成正方体,使S成为正方体的一个顶点,则正三棱锥S-ABC的外接球也即是正方体的外接球,根据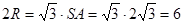 得,R=3,所以正三棱锥S-ABC的外接球的表面积为
得,R=3,所以正三棱锥S-ABC的外接球的表面积为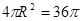 ,结果选(B)。
,结果选(B)。
考点:本题主要考查正三棱锥及球的几何特征,球表面积计算。
点评:在解题过程,反映了正方体问题求解中的“嵌”与“补”,是一种重要的解题技巧,体现了立体几何的较高的能力要求。

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
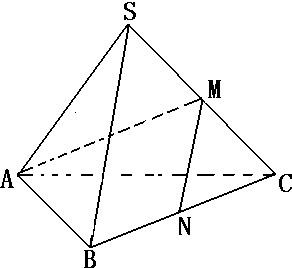 如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=
如图,在正三棱锥S-ABC中,M、N分别为棱SC、BC的中点,并且AM⊥MN,若侧棱长SA=| 3 |
| A、9π | B、12π |
| C、16π | D、32π |
 ,则正三棱锥S-ABC的外接球的表面积为( )
,则正三棱锥S-ABC的外接球的表面积为( )
 ,则正三棱锥S-ABC的外接球的表面积为( )
,则正三棱锥S-ABC的外接球的表面积为( )