题目内容
5.(Ⅰ)如果方程x2+ky2=2表示焦点在y轴上的椭圆,求实数k的取值范围;(Ⅱ)已知双曲线的中心在原点,两个焦点为F1 (-$\sqrt{5}$,0)和F2 ($\sqrt{5}$,0),P在双曲线上,满足$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0且△F1PF2的面积为1,求此双曲线的方程.
分析 (Ⅰ)方程x2+ky2=2可化为$\frac{{y}^{2}}{\frac{2}{k}}+\frac{{x}^{2}}{2}=1$,利用方程x2+ky2=2表示焦点在y轴上的椭圆,建立不等式,即可求实数k的取值范围;
(Ⅱ)设|PF1|=x,|PF2|=y,根据足$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0判断出∠PF1F2=90°进而根据三角形面积公式求得xy,最后根据勾股定理求得x2+y2的值,进而求得y-x,根据双曲线定义求得a,最后根据a和c求得b,双曲线方程可得.
解答 解:(Ⅰ)方程x2+ky2=2可化为$\frac{{y}^{2}}{\frac{2}{k}}+\frac{{x}^{2}}{2}=1$,
∵表示焦点在y轴上的椭圆,
∴$\frac{2}{k}$>2,
∴0<k<1;
(Ⅱ)设|PF1|=x,|PF2|=y,x>y,
∵$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=0,
∴∠PF1F2=90°,
∴$\frac{1}{2}$xy=1,xy=2,
∵F1F1=2$\sqrt{5}$,
∴x2+y2=20,
∴y-x=$\sqrt{{x}^{2}+{y}^{2}-2xy}$=4,
∵y-x=2a=4,
∴a=2,
∴b=1.
∴双曲线方程为$\frac{{x}^{2}}{4}-{y}^{2}=1$.
点评 本题主要考查了椭圆、双曲线的标准方考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
15.如图,一个平面图形的斜二测画法的直观图是一个边长为a的正方形,则原平面图形的面积为( )
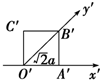

| A. | $\frac{\sqrt{2}}{4}$a2 | B. | a2 | C. | 2$\sqrt{2}$a2 | D. | 2a2 |
20.设等比数列{an}的前n项和为Sn,且S5=10,S10=30,则S15=( )
| A. | 60 | B. | 70 | C. | 90 | D. | 40 |
10.对于函数y=f(x)图象上任意一点P(x1,y1),存在Q(x2,y2),使得x1x2+y1y2=0,则函数y=f(x)可以为( )
| A. | y=2x-2 | B. | y=log2x | C. | y=x2+1 | D. | y=x+1 |