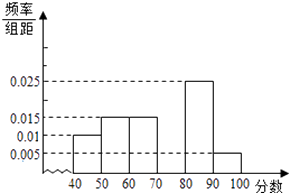
题目内容
【题目】在正方体ABCD﹣A1B1C1D1中： （Ⅰ）求证：AC∥平面A1BC1；
（Ⅱ）求证：平面A1BC1⊥平面BB1D1D．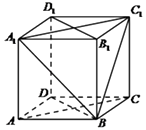
【答案】证明：（Ⅰ）因为AA1∥CC1 ， 所以四边形ACC1A1为平行四边形， 所以AC∥A1C1 ， 又A1C1平面A1BC1 ， AC平面A1BC1 ， AC∥平面A1BC1；
（Ⅱ）易知A1C1⊥B1D1 ， 因为BB1⊥平面A1B1C1D1 ， 所以BB1⊥A1C1
因为BB1∩B1D1=B1 ， 所以A1C1⊥平面BB1D1D，
因为A1C1平面A1BC1 ， 所以平面A1BC1⊥平面BB1D1D
【解析】（Ⅰ）证明四边形ACC1A1为平行四边形，可得AC∥A1C1 ， 即可证明AC∥平面A1BC1；（Ⅱ）证明A1C1⊥平面BB1D1D，即可证明平面A1BC1⊥平面BB1D1D．
练习册系列答案
相关题目
