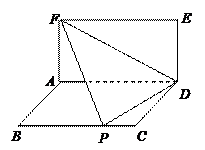题目内容
(本小题满分8分)
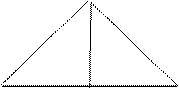
如图,AB是⊙O的直径,C为圆上一点,AB=2,AC=1,P为⊙O所在平面外一点,且PA垂直于⊙O所在平面,PB与⊙O所在平面成角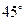 .求点A到平面PBC的距离.
.求点A到平面PBC的距离.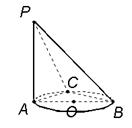
如图,AB是⊙O的直径,C为圆上一点,AB=2,AC=1,P为⊙O所在平面外一点,且PA垂直于⊙O所在平面,PB与⊙O所在平面成角
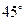 .求点A到平面PBC的距离.
.求点A到平面PBC的距离.

(本小题满分8分)
∵PA⊥平面ABC ∴PA⊥BC.
∵AB是⊙O的直径,C为圆上一点∴BC⊥AC.
∴BC⊥平面PAC
过A作AD⊥PC于D∵BC⊥平面PAC,
BC 平面PBC,
平面PBC,
∴PAC⊥PBC,PC为交线 ∴AD⊥平面PBC
∴AD即为A到平面PBC的距离.
依题意,∠PBA为PB与面ABC所成角,即∠PBA=45°
∴PA=AB=2,AC=1,
可得PC= ∵AD×PC=PA×AC,
∵AD×PC=PA×AC,
∴AD= , 即A到平面PBC的距离为
, 即A到平面PBC的距离为

∵PA⊥平面ABC ∴PA⊥BC.
∵AB是⊙O的直径,C为圆上一点∴BC⊥AC.
∴BC⊥平面PAC
过A作AD⊥PC于D∵BC⊥平面PAC,
BC
 平面PBC,
平面PBC,∴PAC⊥PBC,PC为交线 ∴AD⊥平面PBC
∴AD即为A到平面PBC的距离.
依题意,∠PBA为PB与面ABC所成角,即∠PBA=45°
∴PA=AB=2,AC=1,
可得PC=
 ∵AD×PC=PA×AC,
∵AD×PC=PA×AC,∴AD=
 , 即A到平面PBC的距离为
, 即A到平面PBC的距离为


练习册系列答案
相关题目
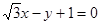 距离的最大值为
距离的最大值为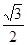
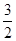
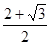
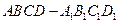 内有一个内切球O,则过棱
内有一个内切球O,则过棱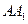 和
和 的中点
的中点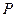 、
、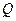 的直线与球面交点为
的直线与球面交点为 、
、 ,则
,则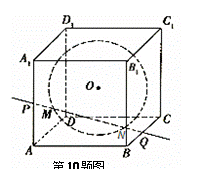
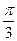
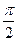
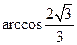
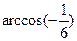
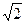 ,CD⊥AB,沿CD将△ABC折成600的二面角A―CD―B ,求折叠后点A到平面BCD的距离。(10分)
,CD⊥AB,沿CD将△ABC折成600的二面角A―CD―B ,求折叠后点A到平面BCD的距离。(10分) 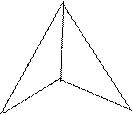
 C. C
C. C  D
D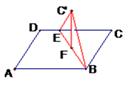

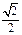
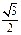
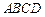 与矩形
与矩形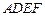 所在的平面互相垂直,将
所在的平面互相垂直,将 沿
沿 翻折,翻折后的点E恰与BC上的点P重合.设
翻折,翻折后的点E恰与BC上的点P重合.设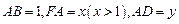 ,则当
,则当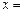 时,
时,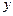 有最小值.
有最小值.