题目内容
设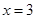 是函数
是函数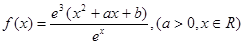 的一个极值点.
的一个极值点.
(1)求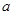 与
与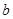 的关系式(用
的关系式(用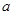 表示
表示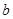 ),并求
),并求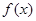 的单调递增区间;
的单调递增区间;
(2)设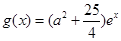 ,若存在
,若存在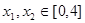 使得
使得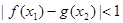 成立,求实数
成立,求实数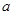 的取值范围.
的取值范围.
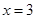 是函数
是函数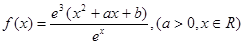 的一个极值点.
的一个极值点.(1)求
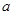 与
与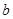 的关系式(用
的关系式(用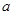 表示
表示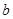 ),并求
),并求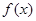 的单调递增区间;
的单调递增区间;(2)设
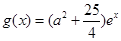 ,若存在
,若存在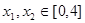 使得
使得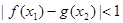 成立,求实数
成立,求实数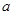 的取值范围.
的取值范围.(1)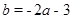 ,
,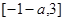 ;(2)
;(2)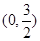 .
.
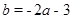 ,
,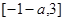 ;(2)
;(2)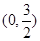 .
.试题分析:(1)先求函数的导函数,根据极值点的导数值为0,可得
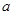 与
与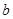 的关系式;再令导函数大于0解不等式得单调递增区间;(2)先根据导数分别求函数
的关系式;再令导函数大于0解不等式得单调递增区间;(2)先根据导数分别求函数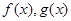 在区间
在区间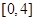 上的最值,代入
上的最值,代入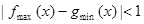 或
或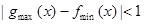 解不等式可得解.
解不等式可得解.试题解析:(1)
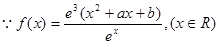 ,
,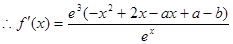 ,
,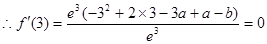 ,
,
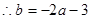 ; (3分)
; (3分)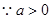 , 令
, 令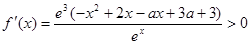 ,即
,即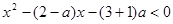
解得:
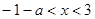 ,所以
,所以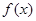 的单调递增区间是:
的单调递增区间是: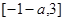 ; (6分)
; (6分)(2)由(1)可得,函数
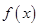 在
在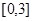 上单调递增,在
上单调递增,在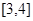 上单调递减,
上单调递减,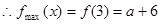 ,且
,且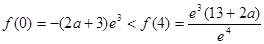
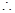 函数
函数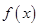 在
在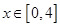 的值域为
的值域为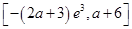 , (8分)
, (8分)又
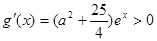
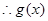 在
在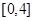 上单调递增,故
上单调递增,故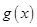 在
在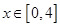 的值域为
的值域为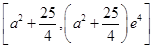 , (10分)
, (10分)若存在
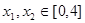 使得
使得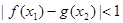 成立,
成立,等价于
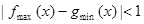 或
或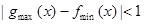 , (13分)
, (13分)又
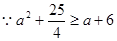 ,
, 于是:
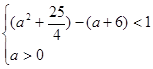 ,解得:
,解得: 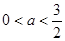 ; (15分)
; (15分)所以实数
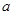 的取值范围是:
的取值范围是: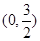 (17分)
(17分)
练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
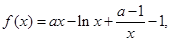 试讨论
试讨论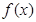 的单调性.
的单调性.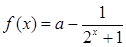 .
.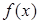 存在零点,求
存在零点,求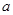 的取值范围
的取值范围 ,使
,使 为奇函数?如果存在,求
为奇函数?如果存在,求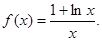
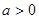 且函数
且函数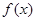 在区间
在区间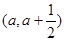 上存在极值,求实数
上存在极值,求实数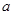 的取值范围;
的取值范围;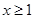 时,不等式
时,不等式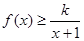 恒成立,求实数
恒成立,求实数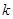 的取值范围.
的取值范围.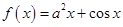 ,
,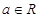 .
. 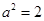 时,求
时,求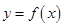 在
在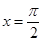 处的切线方程;
处的切线方程;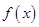 在
在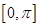 内单调递增,求
内单调递增,求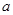 的取值范围.
的取值范围.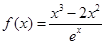 .
.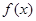 的极大值和极小值;
的极大值和极小值;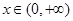 时,
时,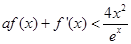 恒成立,求
恒成立,求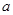 的取值范围.
的取值范围.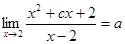 ,且函数
,且函数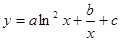 在
在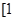 ,
,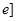 上存在反函数,则( )
上存在反函数,则( )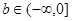
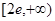
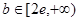
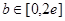
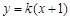 与曲线
与曲线 相切于点
相切于点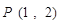 ,则
,则 ________.
________.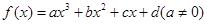 的对称中心为
的对称中心为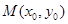 ,记函数
,记函数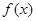 的导函数为
的导函数为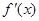 ,
,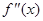 ,则有
,则有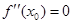 .若函数
.若函数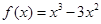 ,则可求得
,则可求得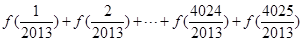 _________.
_________.