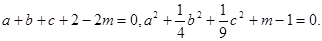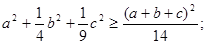题目内容
用数学归纳法证明:
1+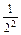 +
+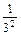 +…+
+…+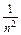 ≥
≥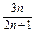 (n∈N*).
(n∈N*).
1+
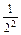 +
+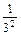 +…+
+…+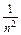 ≥
≥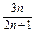 (n∈N*).
(n∈N*).证明略
证明 (1)当n=1时,左边=1,右边=1,
∴左边≥右边,即命题成立.
(2)假设当n=k(k∈N*,k≥1)时,命题成立,
即1+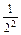 +
+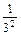 +…+
+…+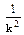 ≥
≥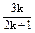 .
.
那么当n=k+1时,要证
1+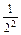 +
+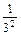 +…+
+…+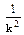 +
+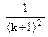 ≥
≥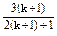 ,
,
只要证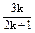 +
+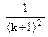 ≥
≥ .
.
∵ -
-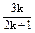 -
-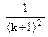 =
=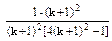
=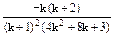 <0,
<0,
∴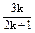 +
+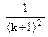 ≥
≥ 成立,
成立,
即1+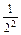 +
+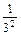 +…+
+…+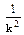 +
+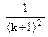 ≥
≥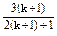 成立.
成立.
∴当n=k+1时命题成立.
由(1)、(2)知,不等式对一切n∈N*均成立.
∴左边≥右边,即命题成立.
(2)假设当n=k(k∈N*,k≥1)时,命题成立,
即1+
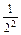 +
+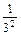 +…+
+…+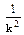 ≥
≥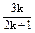 .
.那么当n=k+1时,要证
1+
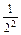 +
+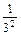 +…+
+…+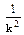 +
+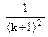 ≥
≥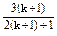 ,
,只要证
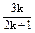 +
+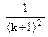 ≥
≥ .
.∵
 -
-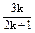 -
-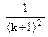 =
=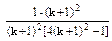
=
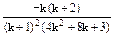 <0,
<0,∴
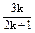 +
+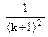 ≥
≥ 成立,
成立,即1+
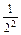 +
+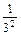 +…+
+…+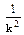 +
+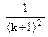 ≥
≥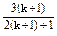 成立.
成立.∴当n=k+1时命题成立.
由(1)、(2)知,不等式对一切n∈N*均成立.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
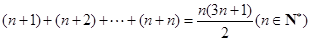
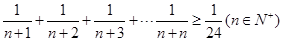 由
由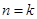 到
到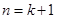 时,不等式左边应添加的项是( )
时,不等式左边应添加的项是( )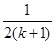
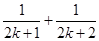
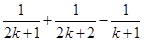
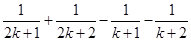
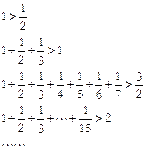
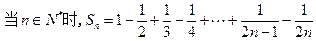
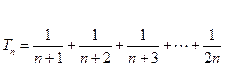
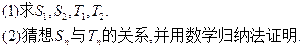
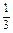 )(1+
)(1+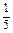 )…(1+
)…(1+ )>
)>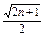 均成立.
均成立.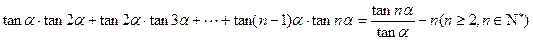
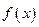 是定义域为正整数集的函数,对于定义域内任意的
是定义域为正整数集的函数,对于定义域内任意的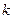 ,若
,若 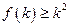 成立,则
成立,则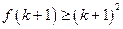 成立,下列命题成立的是
成立,下列命题成立的是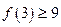 成立,则对于任意
成立,则对于任意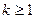 ,均有
,均有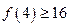 成立,则对于任意的
成立,则对于任意的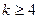 ,均有
,均有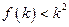 成立;
成立;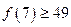 成立,则对于任意的
成立,则对于任意的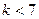 ,均有
,均有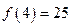 成立,则对于任意的
成立,则对于任意的 是将平面上每个点
是将平面上每个点 的横坐标乘
的横坐标乘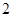 ,纵坐标乘
,纵坐标乘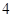 ,变到点
,变到点 .
.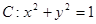 在变换
在变换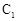 的极坐标方程为:
的极坐标方程为: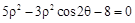 ,直线
,直线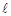 的参数方程为:
的参数方程为: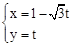 (
(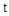 为参数).
为参数).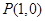 ,曲线
,曲线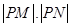 的值.
的值. 为实数,且
为实数,且