题目内容
f′（x0）=0是可导函数y=f（x）在点x=x0处有极值的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、非充分非必要条件 |
考点：利用导数研究函数的极值,必要条件、充分条件与充要条件的判断
专题：导数的综合应用
分析：函数y=f（x）在点x=x0处有极值，则f′（x0）=0；反之不一定，举例反f（x）=x3，虽然f′（0）=0，但是函数f（x）在x=0处没有极值．即可判断出．
解答：
解：若函数y=f（x）在点x=x0处有极值，则f′（x0）=0；
反之不一定，例如取f（x）=x3，虽然f′（0）=0，但是函数f（x）在x=0处没有极值．
因此f′（x0）=0是可导函数y=f（x）在点x=x0处有极值的必要非充分条件．
故选：B．
反之不一定，例如取f（x）=x3，虽然f′（0）=0，但是函数f（x）在x=0处没有极值．
因此f′（x0）=0是可导函数y=f（x）在点x=x0处有极值的必要非充分条件．
故选：B．
点评：本题考查了函数取得极值的充要条件，考查了推理能力与计算能力，属于基础题．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
已知点A（3，3），B（-1，5），直线y=ax+1与线段AB有公共点，则实数α应满足的条件是（ ）
A、α∈[-4，
| ||||||
B、α≠-
| ||||||
C、α∈[-4，-
| ||||||
D、α∈(-∞，-4]∪[
|
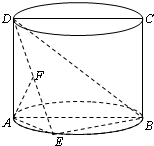如图，圆柱的轴截面ABCD是正方形，点E在底面圆周上（点E异于A、B两点），点F在DE上，且AF⊥DE，若圆柱的底面积与△ABE的面积之比等于π．
如图是某研究性学习小组对全班50人的情商进行调查，按照区间进行分组，得到的情商的分布图，则情商在90-105的人数为