题目内容
在某校教师趣味投篮比赛中,比赛规则是:每场投6个球,至少投进4个球且最后2个球都投进者获奖;否则不获奖.已知教师甲投进每个球的概率都是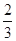 .
.
(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率.
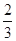 .
.(Ⅰ)记教师甲在每场的6次投球中投进球的个数为X,求X的分布列及数学期望;
(Ⅱ)求教师甲在一场比赛中获奖的概率.
(Ⅰ)X的分布列
数学期望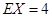 ;(Ⅱ)
;(Ⅱ)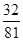 .
.
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P | 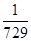 | 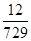 | 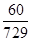 | 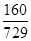 | 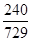 | 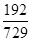 | 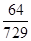 |
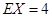 ;(Ⅱ)
;(Ⅱ)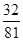 .
.试题分析:(Ⅰ)先定出X的所有可能取值,易知本题是6个独立重复试验中成功的次数的离散概率分布,即为二项分布.由二项分布公式可得到其分布列以及期望.(Ⅱ)根据比赛获胜的规定,教师甲前四次投球中至少有两次投中,后两次必须投中,即可能的情况有1.前四次投中2次(六投四中);2.前四次投中3次(六投五中)3.前四次都投中(六投六中).其中第1种情况有
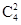 种可能,第2中情况有
种可能,第2中情况有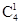 (或
(或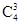 )种可能.将上述三种情况的概率相加即得到教师甲获胜的概率.
)种可能.将上述三种情况的概率相加即得到教师甲获胜的概率.试题解析:(Ⅰ)X的所有可能取值为0,1,2,3,4,5,6.
依条件可知,
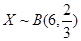
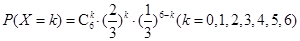 3分
3分X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| P | 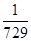 | 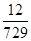 | 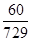 | 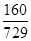 | 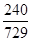 | 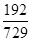 | 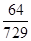 |
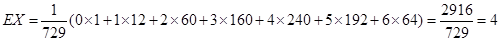 .
.或因为
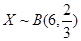 ,所以
,所以 .
.即
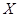 的数学期望为4. 7分
的数学期望为4. 7分(Ⅱ)设教师甲在一场比赛中获奖为事件A,则
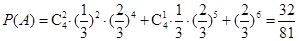 11分
11分答:教师甲在一场比赛中获奖的概率为
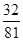 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 店经销
店经销 三种排量的汽车,其中
三种排量的汽车,其中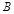 种排量汽车的概率;
种排量汽车的概率;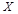 ,求
,求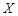 的分布列及数学期望.
的分布列及数学期望.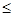 22℃
22℃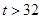 ℃
℃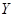
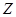
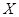 (千元)
(千元)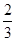 .
. ·0.99k·0.0110-k
·0.99k·0.0110-k







 表示这两人请假次数之和,记“函数
表示这两人请假次数之和,记“函数 在区间
在区间 上有且只有一个零点”为事件
上有且只有一个零点”为事件 ,求事件
,求事件 ;
; 表示这两人请假次数之差的绝对值,求随机变量
表示这两人请假次数之差的绝对值,求随机变量 .
. ,遇到红灯(禁止通行)的概率为
,遇到红灯(禁止通行)的概率为 假定汽车只在遇到红灯或到达目的地才停止前进,
假定汽车只在遇到红灯或到达目的地才停止前进, 表示停车时已经通过的路口数,求:
表示停车时已经通过的路口数,求: